3 Rumus Tinggi Segitiga Paling Mudah Dipahami, Cara Menghitungnya Beserta Penjelasan dan Contoh Soal

MENCARI tinggi segitiga adalah salah satu konsep dasar dalam geometri yang sangat penting untuk dikuasai.

Baik dalam kehidupan sehari-hari maupun dalam ujian matematika, pemahaman tentang rumus tinggi segitiga dapat membantu Anda memecahkan berbagai masalah dengan lebih mudah.

Baca juga : Contoh Soal dan Cara Menghitung Rumus Volume Kubus

Dalam artikel ini, kita akan membahas cara mencari tinggi segitiga, terutama segitiga siku-siku, beserta contoh soal yang mudah dipahami.

Apa Itu Tinggi Segitiga?

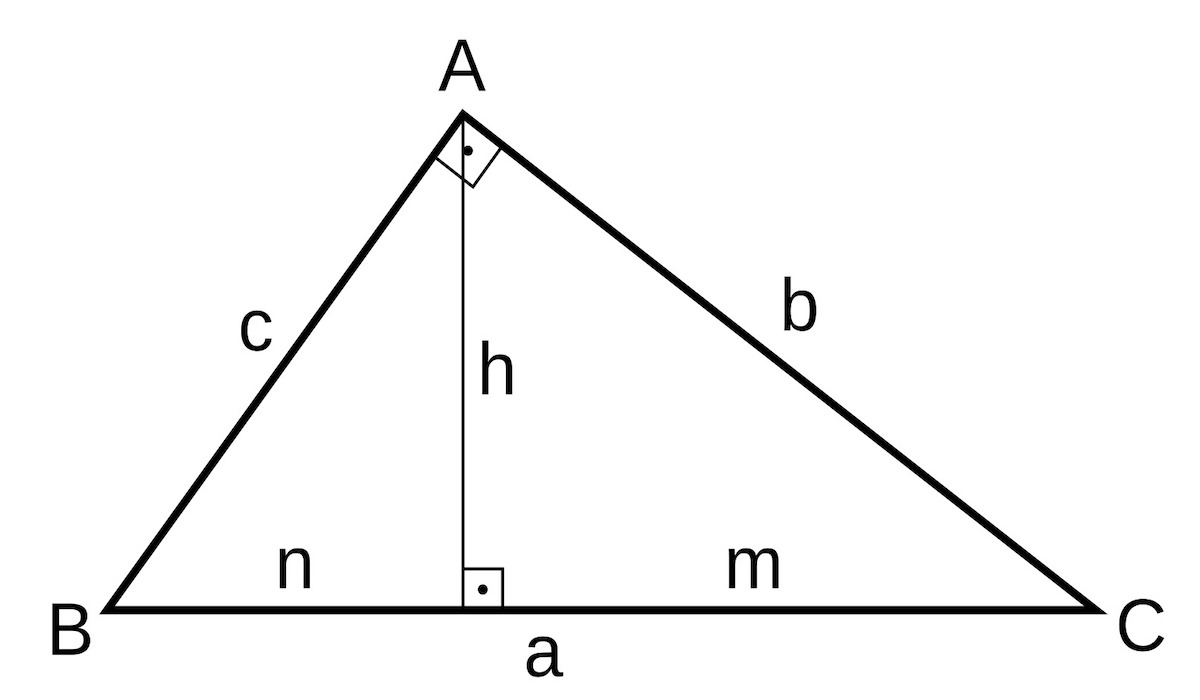
Tinggi segitiga adalah garis lurus yang ditarik dari salah satu sudut segitiga ke sisi yang berseberangan, yang disebut alas, membentuk sudut 90 derajat. Tinggi ini memegang peranan penting dalam berbagai perhitungan geometri, seperti menghitung luas segitiga.

Rumus Mencari Tinggi Segitiga

Ada beberapa cara untuk mencari tinggi segitiga tergantung pada jenis segitiga dan informasi yang tersedia. Berikut adalah rumus dasar yang sering digunakan:

Baca juga : Rumus Matematika SD yang Wajib Dipahami, Cocok untuk Panduan Orang Tua di Rumah

1. Rumus Tinggi Segitiga Umum:

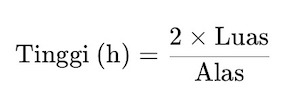
Rumus ini dapat digunakan untuk semua jenis segitiga asalkan luas dan alas diketahui.

2. Rumus Tinggi Segitiga Siku-Siku:

Pada segitiga siku-siku, tinggi dapat ditemukan dengan menggunakan teorema Pythagoras, terutama jika panjang dua sisi lainnya diketahui:

Baca juga : Cara Menghitung Rumus Luas Persegi Panjang, Lengkap dengan Contoh Soalnya

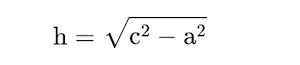
Di mana c adalah sisi miring (hipotenusa), dan a adalah salah satu sisi lainnya.

Baca juga : Memahami Rumus Keliling Lingkaran Beserta 5 Contoh Soalnya

3. Rumus Trigonometri:

Jika salah satu sudut segitiga diketahui, tinggi segitiga juga dapat ditemukan dengan menggunakan rumus trigonometri:

h = b × sin⁡ (A)

Di mana b adalah panjang salah satu sisi dan A adalah sudut yang berhadapan dengan sisi tersebut.

Contoh Soal Mencari Tinggi Segitiga

Mari kita terapkan rumus-rumus di atas melalui beberapa contoh soal:

Contoh Soal 1:

Diketahui sebuah segitiga dengan luas 24 cm² dan alas sepanjang 6 cm. Tentukan tinggi segitiga tersebut.

Penyelesaian: Menggunakan rumus umum:

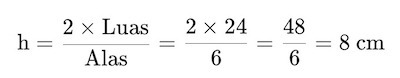
Jadi, tinggi segitiga adalah 8 cm.

Contoh Soal 4:

Sebuah segitiga sama kaki memiliki alas sepanjang 10 cm dan kedua sisi lainnya masing-masing sepanjang 13 cm. Hitung tinggi segitiga tersebut.

Penyelesaian: Segitiga sama kaki dapat dibagi menjadi dua segitiga siku-siku kecil dengan alas 5 cm (setengah dari alas asli). Gunakan teorema Pythagoras:

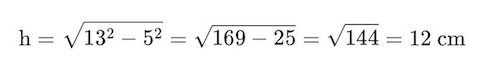
Jadi, tinggi segitiga sama kaki tersebut adalah 12 cm.

Contoh Soal 3:

Diketahui sebuah segitiga dengan alas 9 cm dan sudut di hadapan alas adalah 30 derajat. Panjang sisi lainnya adalah 15 cm. Cari tinggi segitiga tersebut menggunakan rumus trigonometri.

Penyelesaian: Menggunakan rumus trigonometri:

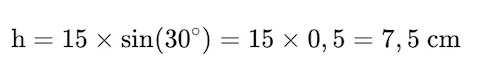
Jadi, tinggi segitiga adalah 7,5 cm.

Contoh Soal 4:

Diketahui sebuah segitiga dengan sisi miring (hipotenusa) sepanjang 17 cm dan salah satu sisi lainnya sepanjang 8 cm. Hitung tinggi segitiga siku-siku tersebut.

Penyelesaian: Gunakan teorema Pythagoras:

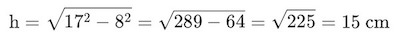
Jadi, tinggi segitiga siku-siku tersebut adalah 15 cm.

Contoh Soal 5:

Sebuah segitiga memiliki tinggi yang sama dengan panjang alasnya, dan luas segitiga tersebut adalah 32 cm². Tentukan panjang alas dan tinggi segitiga tersebut.

Penyelesaian: Misalkan panjang alas = tinggi = x. Luas segitiga:

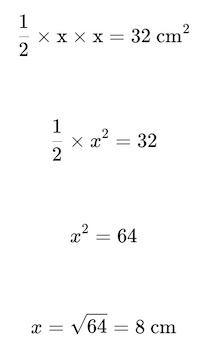
Jadi, panjang alas dan tinggi segitiga tersebut masing-masing adalah 8 cm.

Dengan berbagai contoh soal ini, Anda bisa lebih memahami konsep mencari tinggi segitiga dalam berbagai situasi. Latihan yang konsisten akan membantu memperkuat pemahaman dan keterampilan Anda dalam memecahkan soal-soal matematika.

Pentingnya Memahami Rumus Tinggi Segitiga

Memahami dan menguasai cara mencari tinggi segitiga sangat penting, terutama dalam menyelesaikan soal-soal ujian matematika. Penggunaan rumus yang tepat dapat menghemat waktu dan memastikan jawaban yang akurat.

Selain itu, pemahaman ini juga membantu dalam memahami konsep-konsep geometri yang lebih kompleks.

Mencari tinggi segitiga adalah salah satu keterampilan dasar dalam matematika yang harus dikuasai.

Dengan memahami berbagai rumus dan cara perhitungan, Anda dapat menyelesaikan berbagai masalah geometri dengan lebih efektif. Jangan lupa untuk terus berlatih dengan berbagai contoh soal untuk memperkuat pemahaman Anda. (Z-10)