Ini Rumus Mencari Keliling dan Luas Setengah Lingkaran Serta Contoh Soal

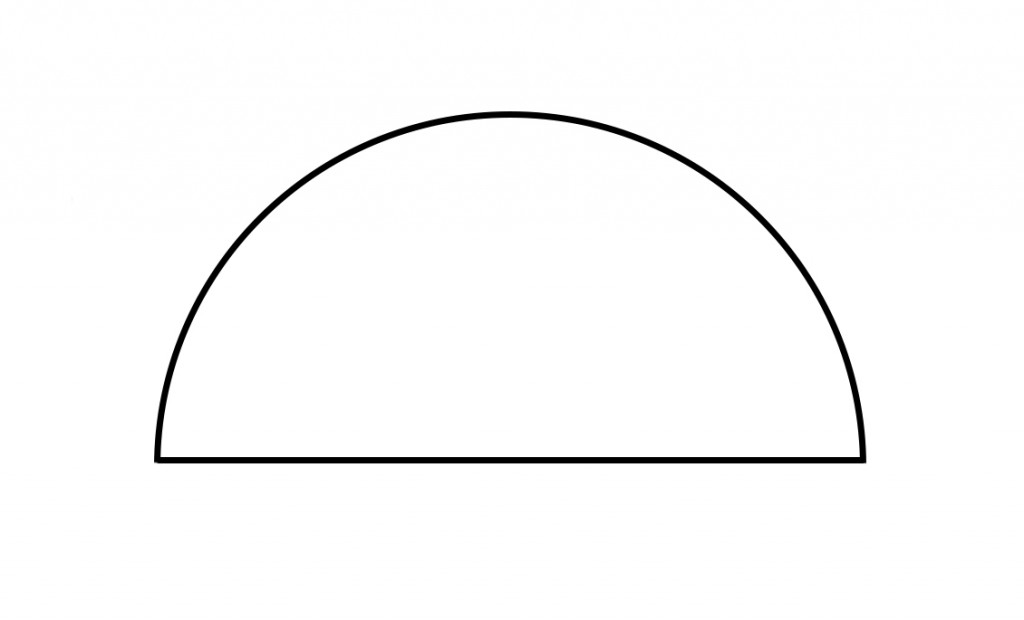
LINGKARAN adalah kurva yang ujung-ujungnya berjarak sama dari pusat. Lokasi suatu titik pada bidang berjarak sama dari suatu titik tertentu pada bidang tersebut. 

Titik khusus ini disebut pusat lingkaran. Lingkaran adalah bentuk yang sangat simetris. Setiap garis yang melalui pusat membentuk garis simetri cermin dan setiap sudut simetris secara rotasi terhadap pusat.

Baca juga: Rumus Volume Bangun Ruang dan Luas Bangun Datar

Untuk menghitung sebuah lingkaran, terdapat rumus yang bisa Anda pelajari. Yaitu luas, dan kelilingnya. Maka, apa saja rumus tersebut, simak terus artikel berikut.

Rumus keliling setengah lingkaran

Sebelum mengetahui rumus keliling setengah lingkaran, perlu bagi kita untuk mengetahui rumus keliling lingkaran. Maka, rumus keliling lingkaran dapat dirumuskan sebagai berikut.

K = 2πr atau K = πd

Dengan 

K : Keliling lingkaran

π (phi) : 3,14 / 22/7

r : jari jari lingkaran

d : diameter lingkaran

Maka, rumus dari keliling setengah lingkaran adalah sebagai berikut.
 
Luas Setengah (1/2) Lingkaran = 1/2 x π x r2

Dengan 

K : Keliling lingkaran

π (phi) : 3,14 / 22/7

r : jari jari lingkaran

Rumus luas setengah lingkaran

Lebih lanjut, untuk mengetahui rumus luas setengah lingkaran, maka penting untuk mengetahui rumus luas lingkaran. Rumus luas lingkaran dapat diuraikan sebagai berikut.

L = πr2

Dengan 

L : Luas lingkaran

π (phi) : 3,14 / 22/7

r : jari jari lingkaran

Maka, rumus luas setengah lingkaran adalah sebagai berikut.

L = ½ x Luas lingkaran (L)

Dengan 

L : Luas lingkaran

π (phi) : 3,14 / 22/7

r : jari jari lingkaran

Contoh soal

Menyelesaikan soal luas setengah lingkaran

Sebuah lingkaran memiliki jari-jari 15 cm. Jika lingkaran tersebut dibagi menjadi dua (2) bagian berapakah luas setengah (1/2) lingkaran tersebut? (π = 3,14)

Jawab:

Diketahui:

r = 15 cm

π = 3,14

Ditanyakan:

Luas setengah (1/2) lingkaran ... 

Penyelesaian:

gunakan rumus menghitung luas setengah (1/2) lingkaran,
 
Luas Setengah (1/2) Lingkaran = 1/2 x π x r2
 
masukkan nilai yang diketahui ke dalam rumus,
 
 Luas Setengah (1/2) Lingkaran = 1/2 x π x r2
                                                   = 1/2 x 3,14 x 152
                                                   = 1/2 x 3,14 x 225
                                                   = 353.25 cm2
 
Jadi, luas setengah lingkaran tersebut adalah 353.25 cm2

Menyelesaikan soal keliling setengah lingkaran

Jika diameter setengah lingkaran tersebut sebesar 16 cm dan π = 22/7. Tentukan keliling setengah lingkaran tersebut.

Jawab:

Diketahui:

d = 16 cm | r = 8 cm

maka

r = 14/2 = 7 cm

π = 22/7
 
Ditanyakan:

Keliling setengah lingkaran ... ?

Penyelesaian:

gunakan rumus menghitung keliling setengah lingkaran,
 
Keliling Setengah (1/2) Lingkaran = π x r
 
masukkan nilai yang diketahui ke dalam rumus
 
Keliling Setengah (1/2) Lingkaran = 22/7 x 8
                                                        = 25 cm
 
Jadi, keliling setengah lingkaran tersebut adalah 25 cm (OL-1)