DALAM pelajaran Fisika SMA, khususnya pada bab Optik Geometri, materi tentang cermin lengkung (sferis) sering menjadi topik yang menantang namun sangat penting. Cermin cekung dan cermin cembung memiliki karakteristik unik yang tidak hanya relevan di atas kertas ujian, tetapi juga dalam aplikasi kehidupan sehari-hari, mulai dari kaca rias, lampu sorot mobil, hingga kaca spion tikungan jalan.
Artikel ini akan mengupas tuntas konsep dasar, sinar-sinar istimewa, rumus perhitungan, hingga cara mudah menentukan sifat bayangan menggunakan Dalil Esbach.
1. Cermin Cekung (Konvergen)
Cermin cekung adalah cermin yang permukaan pantulnya melengkung ke dalam. Cermin ini bersifat konvergen, artinya mengumpulkan berkas sinar cahaya yang datang padanya. Titik fokus (f) pada cermin cekung bernilai positif (nyata) dan terletak di depan cermin.
Sinar Istimewa pada Cermin Cekung
Untuk melukis pembentukan bayangan, kita menggunakan tiga sinar istimewa:
- Sinar datang sejajar sumbu utama dipantulkan melalui titik fokus (f).
- Sinar datang melalui titik fokus (f) dipantulkan sejajar sumbu utama.
- Sinar datang melalui titik pusat kelengkungan (R) dipantulkan kembali melalui titik tersebut.
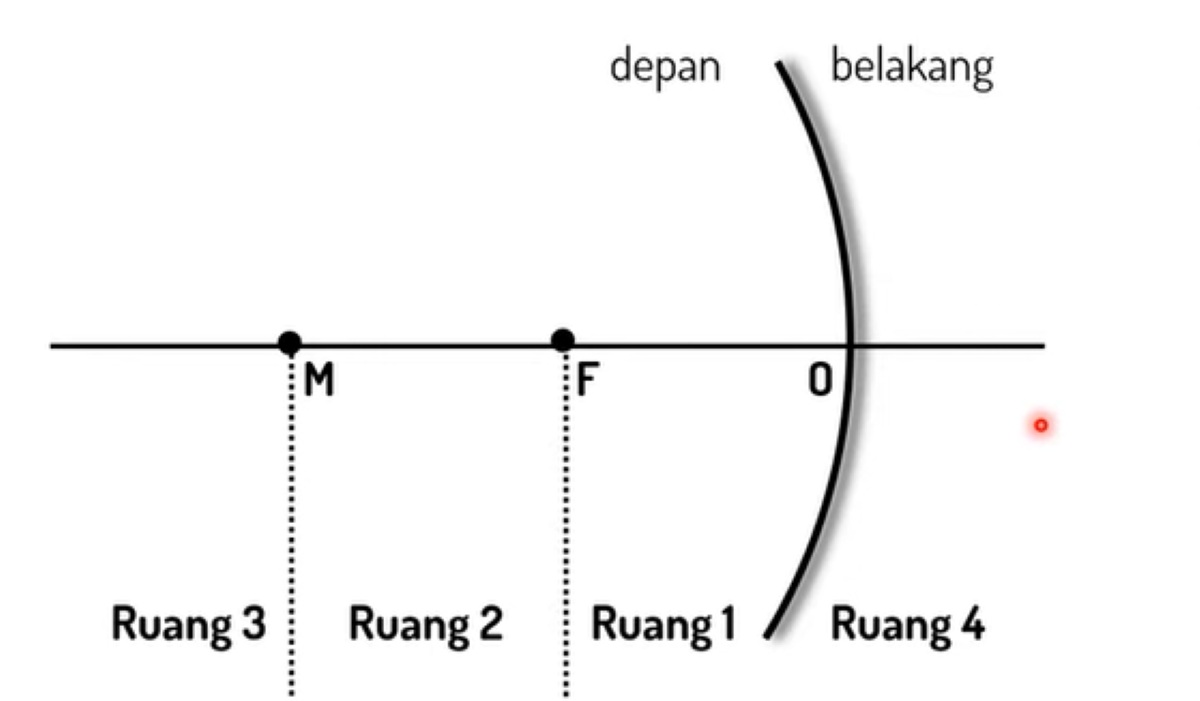
Pembagian Ruang dan Sifat Bayangan
Sifat bayangan pada cermin cekung bergantung pada posisi benda. Berikut ketentuannya:
- Benda di Ruang I (antara O dan f): Bayangan di Ruang IV (Maya, Tegak, Diperbesar).
- Benda di Ruang II (antara f dan R): Bayangan di Ruang III (Nyata, Terbalik, Diperbesar).
- Benda di Ruang III (lebih dari R): Bayangan di Ruang II (Nyata, Terbalik, Diperkecil).
- Benda tepat di R (Pusat Kelengkungan): Bayangan di R (Nyata, Terbalik, Sama Besar).
2. Cermin Cembung (Divergen)
Cermin cembung adalah cermin yang permukaan pantulnya melengkung ke luar. Cermin ini bersifat divergen atau menyebarkan sinar. Titik fokus (f) pada cermin cembung bernilai negatif (maya) dan terletak di belakang cermin. Contoh paling umum adalah kaca spion kendaraan.
Sinar Istimewa pada Cermin Cembung
- Sinar datang sejajar sumbu utama dipantulkan seolah-olah berasal dari titik fokus (f).
- Sinar datang menuju titik fokus (f) dipantulkan sejajar sumbu utama.
- Sinar datang menuju titik pusat kelengkungan (R) dipantulkan kembali seolah-olah berasal dari titik tersebut.
Sifat Bayangan Cermin Cembung
Berbeda dengan cermin cekung yang variatif, sifat bayangan pada cermin cembung untuk benda nyata di depan cermin SELALU:
Maya, Tegak, dan Diperkecil.
3. Rumus Cermin Lengkung dan Perjanjian Tanda
Rumus yang digunakan untuk cermin cekung dan cembung pada dasarnya sama, namun penggunaan tanda positif dan negatif sangat krusial.
Rumus Jarak Fokus dan Bayangan
Hubungan antara jarak fokus (f), jarak benda (s), dan jarak bayangan (s') adalah:
1/f = 1/s + 1/s'
Dimana:
f = Jarak fokus (cm)
s = Jarak benda (cm)
s' = Jarak bayangan (cm)
R = Jari-jari kelengkungan (R = 2f)
Rumus Perbesaran (Magnifikasi)
M = |s' / s| = |h' / h|
Dimana:
M = Perbesaran
h = Tinggi benda
h' = Tinggi bayangan
Perjanjian Tanda (PENTING!)
| Variabel | Bernilai Positif (+) | Bernilai Negatif (-) |
|---|---|---|
| Fokus (f) | Cermin Cekung | Cermin Cembung |
| Jarak Bayangan (s') | Bayangan Nyata (Depan Cermin) | Bayangan Maya (Belakang Cermin) |
| Perbesaran (M) | Bayangan Tegak | Bayangan Terbalik (biasanya ditandai minus pada h') |
4. Trik Cepat: Dalil Esbach
Untuk memprediksi letak dan sifat bayangan tanpa menghitung, gunakan aturan penjumlahan ruang:
Ruang Benda + Ruang Bayangan = 5
- Jika Ruang Bayangan > Ruang Benda = Diperbesar.
- Jika Ruang Bayangan < Ruang Benda = Diperkecil.
- Bayangan di Ruang I & IV = Maya, Tegak.
- Bayangan di Ruang II & III = Nyata, Terbalik.
5. Contoh Soal dan Pembahasan
Contoh Soal 1: Cermin Cekung
Sebuah benda setinggi 4 cm diletakkan 15 cm di depan cermin cekung yang memiliki jari-jari kelengkungan 20 cm. Tentukan jarak bayangan dan sifatnya!
Diketahui:
s = 15 cm
R = 20 cm → f = 10 cm (Positif karena cermin cekung)
h = 4 cm
Jawab:
1/f = 1/s + 1/s'
1/10 = 1/15 + 1/s'
1/s' = 1/10 - 1/15
1/s' = 3/30 - 2/30
1/s' = 1/30
s' = 30 cm
Analisis Sifat: Karena s' bernilai positif, maka bayangan bersifat Nyata dan Terbalik. Karena s' (30) > s (15), maka bayangan Diperbesar.
Contoh Soal 2: Cermin Cembung
Sebuah benda diletakkan 10 cm di depan cermin cembung dengan jarak fokus 10 cm. Tentukan letak bayangannya.
Diketahui:
s = 10 cm
f = -10 cm (Negatif karena cermin cembung)
Jawab:
1/f = 1/s + 1/s'
-1/10 = 1/10 + 1/s'
1/s' = -1/10 - 1/10
1/s' = -2/10
s' = -10/2
s' = -5 cm
Analisis Sifat: Tanda negatif menunjukkan bayangan terletak di belakang cermin, sehingga sifatnya Maya, Tegak, dan Diperkecil.