Luas Belah Ketupat: Rumus dan Contoh Soal Mudah

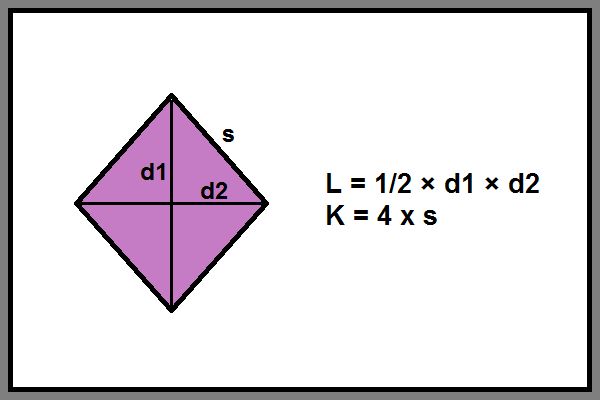
Belah ketupat, sebuah bangun datar dua dimensi yang termasuk dalam kategori segi empat, memiliki karakteristik unik yang membedakannya dari bangun datar lainnya. Keistimewaan belah ketupat terletak pada keempat sisinya yang sama panjang, menjadikannya bentuk yang simetris dan menarik untuk dipelajari. Selain itu, belah ketupat juga memiliki dua diagonal yang saling berpotongan tegak lurus, yang membagi bangun datar ini menjadi empat segitiga siku-siku yang kongruen. Sifat-sifat inilah yang menjadi dasar dalam perhitungan luas belah ketupat.

Memahami Konsep Luas Belah Ketupat

Luas suatu bangun datar, termasuk belah ketupat, pada dasarnya adalah ukuran seberapa besar permukaan yang ditempati oleh bangun datar tersebut. Dalam konteks belah ketupat, luasnya dapat dihitung dengan memanfaatkan panjang diagonal-diagonalnya. Diagonal belah ketupat adalah garis lurus yang menghubungkan dua sudut yang berhadapan. Karena diagonal-diagonal belah ketupat saling berpotongan tegak lurus, maka mereka membagi belah ketupat menjadi empat segitiga siku-siku yang identik. Dengan memahami hubungan antara diagonal dan luas segitiga siku-siku, kita dapat menurunkan rumus untuk menghitung luas belah ketupat secara keseluruhan.

Rumus luas belah ketupat sangat sederhana dan mudah diingat, yaitu:

Baca juga : Simbol Matematika: Definisi dan Contoh Penggunaan

Luas = 1/2 × d1 × d2

Di mana d1 dan d2 adalah panjang diagonal-diagonal belah ketupat.

Rumus ini menunjukkan bahwa luas belah ketupat sama dengan setengah dari hasil perkalian panjang kedua diagonalnya. Dengan mengetahui panjang kedua diagonal belah ketupat, kita dapat dengan mudah menghitung luasnya menggunakan rumus ini.

Baca juga : Luas Permukaan Limas: Rumus dan Contoh Soal

Menurunkan Rumus Luas Belah Ketupat

Untuk memahami mengapa rumus luas belah ketupat berbentuk seperti itu, mari kita tinjau proses penurunannya. Seperti yang telah disebutkan sebelumnya, belah ketupat dapat dibagi menjadi empat segitiga siku-siku yang kongruen oleh diagonal-diagonalnya. Luas setiap segitiga siku-siku dapat dihitung dengan rumus:

Luas segitiga siku-siku = 1/2 × alas × tinggi

Dalam konteks belah ketupat, alas dan tinggi setiap segitiga siku-siku adalah setengah dari panjang diagonal-diagonal belah ketupat. Jadi, luas setiap segitiga siku-siku adalah:

Baca juga : Rumus Luas Permukaan Limas: Panduan Lengkap untuk Anda

Luas segitiga siku-siku = 1/2 × (1/2 × d1) × (1/2 × d2) = 1/8 × d1 × d2

Karena ada empat segitiga siku-siku yang identik, maka luas belah ketupat adalah empat kali luas setiap segitiga siku-siku:

Luas belah ketupat = 4 × (1/8 × d1 × d2) = 1/2 × d1 × d2

Baca juga : Perkalian Matriks: Dasar-Dasar yang Harus Dikuasai

Dengan demikian, kita telah membuktikan bahwa rumus luas belah ketupat adalah 1/2 × d1 × d2.

Contoh Soal dan Pembahasan

Untuk memperjelas pemahaman tentang cara menghitung luas belah ketupat, berikut adalah beberapa contoh soal beserta pembahasannya:

Contoh Soal 1:

Sebuah belah ketupat memiliki panjang diagonal 12 cm dan 16 cm. Hitunglah luas belah ketupat tersebut.

Pembahasan:

Diketahui: d1 = 12 cm, d2 = 16 cm

Luas = 1/2 × d1 × d2 = 1/2 × 12 cm × 16 cm = 96 cm²

Jadi, luas belah ketupat tersebut adalah 96 cm².

Contoh Soal 2:

Luas sebuah belah ketupat adalah 150 cm². Jika panjang salah satu diagonalnya adalah 15 cm, hitunglah panjang diagonal yang lain.

Pembahasan:

Diketahui: Luas = 150 cm², d1 = 15 cm

Luas = 1/2 × d1 × d2

150 cm² = 1/2 × 15 cm × d2

d2 = (150 cm² × 2) / 15 cm = 20 cm

Jadi, panjang diagonal yang lain adalah 20 cm.

Contoh Soal 3:

Sebuah taman berbentuk belah ketupat akan ditanami rumput. Panjang diagonal-diagonal taman tersebut adalah 20 m dan 25 m. Jika harga rumput adalah Rp 50.000 per meter persegi, hitunglah biaya yang dibutuhkan untuk menanami seluruh taman dengan rumput.

Pembahasan:

Diketahui: d1 = 20 m, d2 = 25 m, harga rumput = Rp 50.000/m²

Luas taman = 1/2 × d1 × d2 = 1/2 × 20 m × 25 m = 250 m²

Biaya yang dibutuhkan = Luas taman × harga rumput = 250 m² × Rp 50.000/m² = Rp 12.500.000

Jadi, biaya yang dibutuhkan untuk menanami seluruh taman dengan rumput adalah Rp 12.500.000.

Sifat-Sifat Belah Ketupat yang Perlu Diketahui

Selain rumus luas, penting juga untuk memahami sifat-sifat belah ketupat yang mendasarinya. Berikut adalah beberapa sifat penting belah ketupat:

• Keempat sisinya sama panjang.
• Sudut-sudut yang berhadapan sama besar.
• Diagonal-diagonalnya saling berpotongan tegak lurus.
• Diagonal-diagonalnya saling membagi dua sama panjang.
• Diagonal-diagonalnya merupakan garis sumbu simetri.
• Belah ketupat memiliki simetri putar tingkat dua.
• Belah ketupat dapat menutupi bidang secara periodik.

Sifat-sifat ini tidak hanya membantu dalam memahami karakteristik belah ketupat, tetapi juga berguna dalam menyelesaikan berbagai masalah geometri yang melibatkan belah ketupat.

Belah Ketupat dalam Kehidupan Sehari-hari

Belah ketupat bukanlah sekadar konsep matematika abstrak. Bentuk ini sering kita jumpai dalam kehidupan sehari-hari, baik secara alami maupun buatan manusia. Berikut adalah beberapa contoh penerapan belah ketupat dalam kehidupan sehari-hari:

• Layang-layang: Bentuk layang-layang yang tradisional seringkali menyerupai belah ketupat.
• Motif batik: Banyak motif batik tradisional yang menggunakan bentuk belah ketupat sebagai elemen desainnya.
• Ubin lantai: Beberapa desain ubin lantai menggunakan bentuk belah ketupat untuk menciptakan pola yang menarik.
• Rangkaian berlian: Potongan berlian seringkali memiliki bentuk belah ketupat atau kombinasi belah ketupat.
• Logo perusahaan: Beberapa perusahaan menggunakan bentuk belah ketupat dalam logo mereka untuk memberikan kesan modern dan dinamis.
• Dekorasi rumah: Hiasan dinding atau ornamen rumah lainnya terkadang menggunakan bentuk belah ketupat sebagai elemen dekoratif.

Dengan menyadari keberadaan belah ketupat di sekitar kita, kita dapat lebih mengapresiasi keindahan dan kegunaan bentuk geometri ini.

Tips dan Trik dalam Menghitung Luas Belah Ketupat

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam menghitung luas belah ketupat dengan lebih mudah dan efisien:

• Pastikan satuan panjang diagonal sama: Sebelum menghitung luas, pastikan bahwa satuan panjang kedua diagonal sudah sama. Jika tidak, konversikan terlebih dahulu ke satuan yang sama.
• Gunakan kalkulator jika perlu: Jika angka-angka yang terlibat dalam perhitungan cukup besar atau rumit, jangan ragu untuk menggunakan kalkulator untuk menghindari kesalahan perhitungan.
• Periksa kembali jawaban Anda: Setelah mendapatkan hasil perhitungan, periksa kembali jawaban Anda untuk memastikan tidak ada kesalahan.
• Gunakan rumus alternatif jika informasi yang diberikan berbeda: Jika Anda tidak mengetahui panjang kedua diagonal, tetapi mengetahui informasi lain seperti panjang sisi dan salah satu sudut, Anda dapat menggunakan rumus alternatif untuk menghitung luas belah ketupat.
• Latih soal-soal yang bervariasi: Semakin banyak Anda berlatih soal-soal yang bervariasi, semakin mahir Anda dalam menghitung luas belah ketupat.

Dengan mengikuti tips dan trik ini, Anda akan dapat menghitung luas belah ketupat dengan lebih cepat, akurat, dan percaya diri.

Rumus Alternatif untuk Menghitung Luas Belah Ketupat

Selain rumus dasar yang menggunakan panjang diagonal, terdapat juga rumus alternatif untuk menghitung luas belah ketupat, tergantung pada informasi yang tersedia. Berikut adalah beberapa rumus alternatif tersebut:

1. Jika diketahui panjang sisi (s) dan salah satu sudut (θ):

   Luas = s² × sin(θ)

2. Jika diketahui panjang sisi (s) dan tinggi (t):

   Luas = s × t

Rumus-rumus alternatif ini sangat berguna ketika Anda tidak mengetahui panjang kedua diagonal, tetapi memiliki informasi lain yang relevan. Penting untuk memahami kapan dan bagaimana menggunakan rumus-rumus ini dengan tepat.

Perbedaan Belah Ketupat dengan Bangun Datar Lainnya

Belah ketupat seringkali tertukar dengan bangun datar lainnya, seperti persegi, persegi panjang, dan jajar genjang. Meskipun memiliki beberapa kesamaan, belah ketupat memiliki karakteristik unik yang membedakannya dari bangun datar tersebut. Berikut adalah perbedaan utama antara belah ketupat dengan bangun datar lainnya:

• Persegi: Persegi adalah belah ketupat yang semua sudutnya siku-siku. Jadi, persegi adalah kasus khusus dari belah ketupat.
• Persegi Panjang: Persegi panjang memiliki dua pasang sisi yang sama panjang dan semua sudutnya siku-siku. Berbeda dengan belah ketupat yang semua sisinya sama panjang.
• Jajar Genjang: Jajar genjang memiliki dua pasang sisi yang sejajar dan sama panjang, tetapi tidak semua sisinya harus sama panjang seperti belah ketupat.

Dengan memahami perbedaan ini, Anda dapat dengan mudah mengidentifikasi belah ketupat dan membedakannya dari bangun datar lainnya.

Aplikasi Belah Ketupat dalam Bidang Lain

Konsep belah ketupat tidak hanya terbatas pada matematika dan geometri. Bentuk ini juga memiliki aplikasi dalam berbagai bidang lain, seperti:

• Seni dan Desain: Belah ketupat sering digunakan sebagai elemen desain dalam seni, arsitektur, dan desain grafis.
• Teknik: Bentuk belah ketupat dapat ditemukan dalam struktur jembatan, rangka bangunan, dan desain mesin.
• Ilmu Alam: Beberapa kristal mineral memiliki bentuk belah ketupat.
• Permainan: Bentuk belah ketupat digunakan dalam beberapa permainan, seperti catur dan dam.

Dengan memahami aplikasi belah ketupat dalam berbagai bidang, kita dapat lebih menghargai relevansi dan kegunaan konsep ini dalam dunia nyata.

Kesimpulan

Belah ketupat adalah bangun datar yang menarik dan memiliki banyak aplikasi dalam kehidupan sehari-hari. Dengan memahami sifat-sifatnya, rumus luasnya, dan perbedaan dengan bangun datar lainnya, kita dapat dengan mudah menyelesaikan berbagai masalah geometri yang melibatkan belah ketupat. Jangan ragu untuk berlatih soal-soal yang bervariasi dan menerapkan tips dan trik yang telah dibahas untuk meningkatkan kemampuan Anda dalam menghitung luas belah ketupat. Semoga artikel ini bermanfaat dan menambah wawasan Anda tentang belah ketupat. (Z-2)