Rumus Luas Permukaan Limas: Panduan Lengkap untuk Anda

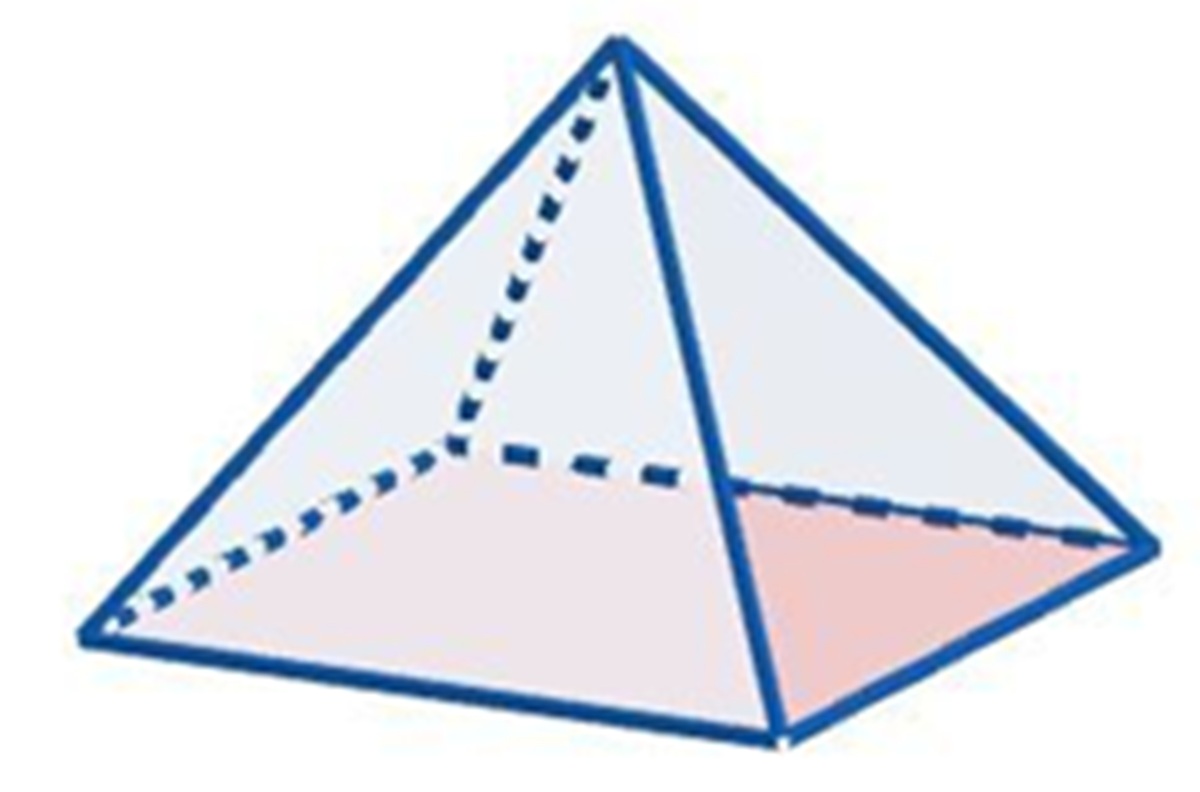
Limas, bangun ruang yang khas dengan alas berbentuk poligon dan sisi-sisi tegak yang bertemu di satu titik puncak, seringkali menjadi tantangan tersendiri dalam geometri. Memahami cara menghitung luas permukaannya adalah keterampilan penting, baik untuk keperluan akademis maupun aplikasi praktis dalam kehidupan sehari-hari. Artikel ini akan mengupas tuntas rumus luas permukaan limas, memberikan panduan langkah demi langkah yang mudah diikuti, serta contoh-contoh soal yang relevan untuk memperdalam pemahaman Anda.

Memahami Komponen Limas

Sebelum melangkah lebih jauh ke dalam perhitungan luas permukaan, penting untuk memahami komponen-komponen dasar yang membentuk sebuah limas. Komponen-komponen ini akan menjadi kunci dalam mengaplikasikan rumus dengan tepat.

Alas Limas: Alas adalah bidang poligon yang menjadi dasar dari limas. Bentuk alas ini bisa beragam, mulai dari segitiga, segi empat, segi lima, hingga poligon dengan sisi yang lebih banyak. Nama limas biasanya mengikuti bentuk alasnya, misalnya limas segitiga jika alasnya berbentuk segitiga, atau limas segi empat jika alasnya berbentuk segi empat.

Baca juga : Perkalian Matriks: Dasar-Dasar yang Harus Dikuasai

Sisi Tegak: Sisi tegak adalah bidang-bidang berbentuk segitiga yang menghubungkan setiap sisi alas dengan titik puncak limas. Jumlah sisi tegak selalu sama dengan jumlah sisi pada alas. Misalnya, limas segi empat memiliki empat sisi tegak.

Titik Puncak: Titik puncak adalah titik di mana semua sisi tegak bertemu. Titik ini terletak di atas alas limas.

Tinggi Limas: Tinggi limas adalah jarak tegak lurus dari titik puncak ke bidang alas. Tinggi ini sangat penting dalam perhitungan volume limas, tetapi tidak secara langsung digunakan dalam perhitungan luas permukaan.

Baca juga : Pendidikan Pasar Modal Bisa Diajarkan di Tingkat Dasar

Garis Tinggi Sisi Tegak (Apotema): Garis tinggi sisi tegak, atau sering disebut apotema sisi tegak, adalah jarak tegak lurus dari titik puncak ke sisi alas pada salah satu sisi tegak. Apotema ini sangat penting dalam menghitung luas setiap sisi tegak.

Rumus Dasar Luas Permukaan Limas

Luas permukaan limas adalah jumlah total luas semua bidang yang membentuk limas tersebut. Ini terdiri dari luas alas dan luas semua sisi tegaknya. Secara matematis, rumus luas permukaan limas dapat dituliskan sebagai berikut:

Luas Permukaan Limas = Luas Alas + Jumlah Luas Sisi Tegak

Baca juga : Ini Tips Mengajarkan Matematika kepada Anak dari Tasya Kamila

Rumus ini berlaku untuk semua jenis limas, terlepas dari bentuk alasnya. Namun, cara menghitung luas alas akan berbeda tergantung pada bentuk alasnya.

Menghitung Luas Alas Limas

Seperti yang telah disebutkan, bentuk alas limas bisa beragam. Oleh karena itu, kita perlu mengetahui cara menghitung luas berbagai jenis poligon yang mungkin menjadi alas limas.

Alas Berbentuk Segitiga: Luas segitiga dihitung dengan rumus:

Baca juga : Jerome Polin Sindir Hukuman Koruptor dan Hitung Pendapatan Koruptor Vonis 6 Tahun Tembus Rp20 Juta per Jam

Luas = 1/2 alas tinggi

Di mana alas adalah panjang sisi alas segitiga, dan tinggi adalah jarak tegak lurus dari sisi alas ke titik sudut yang berlawanan.

Alas Berbentuk Segi Empat: Jika alas berbentuk persegi, maka luasnya adalah:

Luas = sisi sisi

Jika alas berbentuk persegi panjang, maka luasnya adalah:

Luas = panjang lebar

Alas Berbentuk Poligon Beraturan: Untuk poligon beraturan (semua sisi dan sudut sama), seperti segi lima beraturan atau segi enam beraturan, luasnya dapat dihitung dengan rumus:

Luas = 1/2 keliling apotema

Di mana keliling adalah jumlah panjang semua sisi poligon, dan apotema adalah jarak dari pusat poligon ke tengah salah satu sisinya.

Menghitung Luas Sisi Tegak Limas

Setiap sisi tegak limas berbentuk segitiga. Oleh karena itu, luas setiap sisi tegak dihitung dengan rumus luas segitiga:

Luas = 1/2 alas tinggi

Dalam konteks sisi tegak limas, alas adalah panjang sisi alas limas yang menjadi dasar sisi tegak tersebut, dan tinggi adalah apotema sisi tegak (jarak tegak lurus dari titik puncak limas ke sisi alas).

Jika limas memiliki alas yang beraturan dan semua sisi tegaknya kongruen (identik), maka kita hanya perlu menghitung luas satu sisi tegak, kemudian mengalikannya dengan jumlah sisi tegak.

Langkah-Langkah Menghitung Luas Permukaan Limas

Berikut adalah langkah-langkah sistematis untuk menghitung luas permukaan limas:

1. Identifikasi Bentuk Alas: Tentukan bentuk poligon yang menjadi alas limas (segitiga, segi empat, dll.).
2. Hitung Luas Alas: Gunakan rumus yang sesuai untuk menghitung luas alas berdasarkan bentuknya.
3. Hitung Luas Setiap Sisi Tegak: Hitung luas setiap sisi tegak menggunakan rumus luas segitiga (1/2 alas apotema). Pastikan Anda menggunakan apotema yang benar untuk setiap sisi tegak.
4. Jumlahkan Luas Semua Sisi Tegak: Jumlahkan luas semua sisi tegak untuk mendapatkan total luas sisi tegak.
5. Hitung Luas Permukaan Total: Jumlahkan luas alas dengan total luas sisi tegak untuk mendapatkan luas permukaan limas.

Contoh Soal dan Pembahasan

Untuk memperjelas pemahaman Anda, mari kita bahas beberapa contoh soal:

Contoh 1: Sebuah limas segi empat memiliki alas berbentuk persegi dengan sisi 6 cm. Apotema sisi tegaknya adalah 5 cm. Hitunglah luas permukaan limas tersebut.

Pembahasan:

Luas Alas = sisi sisi = 6 cm 6 cm = 36 cm²

Luas Satu Sisi Tegak = 1/2 alas apotema = 1/2 6 cm 5 cm = 15 cm²

Jumlah Luas Sisi Tegak = 4 15 cm² = 60 cm²

Luas Permukaan Limas = Luas Alas + Jumlah Luas Sisi Tegak = 36 cm² + 60 cm² = 96 cm²

Contoh 2: Sebuah limas segitiga memiliki alas berbentuk segitiga sama sisi dengan sisi 8 cm dan tinggi 7 cm. Apotema sisi tegaknya adalah 6 cm. Hitunglah luas permukaan limas tersebut.

Pembahasan:

Luas Alas = 1/2 alas tinggi = 1/2 8 cm 7 cm = 28 cm²

Luas Satu Sisi Tegak = 1/2 alas apotema = 1/2 8 cm 6 cm = 24 cm²

Jumlah Luas Sisi Tegak = 3 24 cm² = 72 cm²

Luas Permukaan Limas = Luas Alas + Jumlah Luas Sisi Tegak = 28 cm² + 72 cm² = 100 cm²

Tips dan Trik dalam Menghitung Luas Permukaan Limas

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam menghitung luas permukaan limas dengan lebih mudah dan akurat:

• Gambar Sketsa: Selalu gambar sketsa limas untuk memvisualisasikan komponen-komponennya dan memahami hubungan antar komponen tersebut.
• Perhatikan Satuan: Pastikan semua satuan pengukuran (panjang, lebar, tinggi, apotema) konsisten sebelum melakukan perhitungan. Jika tidak, konversikan terlebih dahulu ke satuan yang sama.
• Gunakan Kalkulator: Gunakan kalkulator untuk membantu Anda dalam perhitungan, terutama jika angkanya rumit atau melibatkan desimal.
• Periksa Kembali: Setelah selesai menghitung, periksa kembali semua langkah dan perhitungan Anda untuk memastikan tidak ada kesalahan.
• Pahami Konsep: Jangan hanya menghafal rumus, tetapi pahami konsep dasar di balik rumus tersebut. Ini akan membantu Anda dalam memecahkan masalah yang lebih kompleks.

Aplikasi Luas Permukaan Limas dalam Kehidupan Sehari-hari

Meskipun terlihat abstrak, konsep luas permukaan limas memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Berikut adalah beberapa contoh:

• Arsitektur: Arsitek menggunakan perhitungan luas permukaan limas untuk merancang atap bangunan, menara, dan struktur lainnya yang berbentuk limas. Perhitungan ini penting untuk menentukan jumlah material yang dibutuhkan dan memastikan kekuatan struktur.
• Kemasan: Desainer kemasan menggunakan perhitungan luas permukaan limas untuk merancang kotak atau wadah berbentuk limas. Perhitungan ini penting untuk menentukan jumlah material yang dibutuhkan dan memastikan produk terlindungi dengan baik.
• Geografi: Ahli geografi menggunakan perhitungan luas permukaan limas untuk memperkirakan luas permukaan gunung atau bukit yang berbentuk limas.
• Seni dan Kerajinan: Seniman dan pengrajin menggunakan konsep luas permukaan limas untuk membuat karya seni atau kerajinan tangan yang berbentuk limas, seperti piramida mini atau hiasan dekoratif.

Jenis-Jenis Limas dan Karakteristiknya

Limas dapat diklasifikasikan berdasarkan bentuk alasnya. Berikut adalah beberapa jenis limas yang umum:

Limas Segitiga: Limas segitiga memiliki alas berbentuk segitiga. Limas ini juga dikenal sebagai tetrahedron jika semua sisinya berbentuk segitiga sama sisi.

Limas Segi Empat: Limas segi empat memiliki alas berbentuk segi empat. Jika alasnya berbentuk persegi, maka limas tersebut disebut limas persegi.

Limas Segi Lima: Limas segi lima memiliki alas berbentuk segi lima.

Limas Segi Enam: Limas segi enam memiliki alas berbentuk segi enam.

Selain berdasarkan bentuk alasnya, limas juga dapat diklasifikasikan berdasarkan posisi titik puncaknya. Jika titik puncak limas terletak tepat di atas pusat alas, maka limas tersebut disebut limas tegak. Jika titik puncak limas tidak terletak tepat di atas pusat alas, maka limas tersebut disebut limas miring.

Perbedaan Limas dan Prisma

Limas dan prisma adalah dua jenis bangun ruang yang seringkali membingungkan. Berikut adalah beberapa perbedaan utama antara limas dan prisma:

Fitur	Limas	Prisma
Alas	Satu alas	Dua alas yang kongruen dan sejajar
Sisi Tegak	Berbentuk segitiga dan bertemu di satu titik puncak	Berbentuk persegi panjang atau jajar genjang
Titik Puncak	Memiliki satu titik puncak	Tidak memiliki titik puncak

Soal Latihan Tambahan

Untuk menguji pemahaman Anda, coba kerjakan soal-soal latihan berikut:

1. Sebuah limas persegi memiliki sisi alas 10 cm dan apotema sisi tegak 8 cm. Hitunglah luas permukaan limas tersebut.
2. Sebuah limas segitiga sama sisi memiliki sisi alas 12 cm dan tinggi alas 10 cm. Apotema sisi tegaknya adalah 9 cm. Hitunglah luas permukaan limas tersebut.
3. Sebuah limas segi enam beraturan memiliki sisi alas 5 cm dan apotema alas 4.33 cm. Apotema sisi tegaknya adalah 7 cm. Hitunglah luas permukaan limas tersebut.

Kesimpulan

Menghitung luas permukaan limas memang membutuhkan pemahaman tentang komponen-komponen limas dan rumus-rumus yang relevan. Dengan mengikuti langkah-langkah yang telah dijelaskan dan berlatih dengan contoh-contoh soal, Anda akan semakin mahir dalam menghitung luas permukaan limas. Ingatlah untuk selalu memperhatikan bentuk alas limas dan menggunakan rumus yang sesuai untuk menghitung luas alas dan luas sisi tegaknya. Semoga artikel ini bermanfaat dan membantu Anda dalam memahami konsep luas permukaan limas dengan lebih baik. (Z-2)