Bilangan Berpangkat: Definisi dan Contoh Soal

PADA pelajaran matematika di Kelas IX SMP (sekolah menengah pertama) kita akan mempelajari bilangan berpangkat. Akan ada definisi dan sifat-sifat dari bilangan berpangkat.

Apa definisi dan dan bagaimana contoh soal bilangan berpangkat? Untuk lebih jelasnya berikut uraiannya yang dilansir dari buku Matematika Untuk SMP/MTs Kelas IX dengan penulis Subchan dkk.

Definisi

Perpangkatan adalah perkalian berulang dari suatu bilangan yang sama. Bilangan pokok dalam suatu perpangkatan disebut basis. Banyaknya bilangan pokok yang dikalikan secara berulang disebut eksponen atau pangkat.

Baca juga : Berhitung Perkalian dan Pembagian Bilangan Bulat serta Sifat-sifatnya

Berikut bentuk umum dari perpangkatan.

aⁿ = a × a × a × ... × a.

a sebanyak n dengan n bilangan bulat positif.

Baca juga : Daftar Perkalian 1 sampai dengan 20, Berani Hafalkan

a disebut dengan bilangan pokok atau basis, n disebut eksponen atau pangkat.

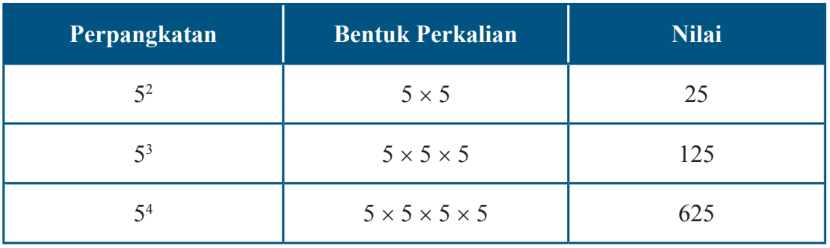
5³ merupakan perpangkatan dari 5. Bilangan 5 merupakan basis atau bilangan pokok. Sedangkan 3 merupakan eksponen atau pangkat.

Contoh soal

a. 3 × 3 × 3 × 3 = 3⁴.

3⁴ disebut perpangkatan 4.

3 disebut sebagai bilangan pokok (basis) sedangkan 4 sebagai pangkat (eksponen).

Baca juga : Pengertian Bilangan Kuadrat serta Hasil Pangkat Dua dari 1 sampai 100

Hasil 3⁴ = 81.

b. (–2) × (–2) × (–2) = (–2)³.

Karena (–2) dikalikan berulang sebanyak tiga kali, (–2) × (–2) × (–2) merupakan perpangkatan dengan basis (–2) dan pangkat 3.

Jadi (–2) × (–2) × (–2) = (–2)³ dapat disebut dengan perpangkatan 3.

Baca juga : Perkembangan Lima Teori Atom oleh para Ilmuwan

(–2) × (–2) × (–2) = (–2)³ = 4 x (–2) = –8.

Jika bilangan negatif dipangkat bilangan ganjil menghasilkan bilangan negatif.

c. (–2) x (–2) x (–2) x (–2) = (–2)⁴ = 4 x 4 = 16.

Jika bilangan negatif dipangkat bilangan genap menghasilkan bilangan positif.

d. –3⁴ = – (3 x 3 x 3 x 3) = – (9 x 9) = 18.

Jadi jika tanda negatif tidak dikurung, tanda negatif itu tidak masuk dalam perpangkatan.

e. Nyatakan perpangkatan (–0,3)² dan (0,3)² dalam bentuk bilangan biasa.

(–0,3)² = (–0,3) × (–0,3) = 0,09.

(0,3)² = (0,3) × (0,3) = 0,09.

f. Nyatakan perpangkatan (–0,3)³ dan (0,3)³ dalam bentuk bilangan biasa.

(–0,3)³ = (–0,3) × (–0,3) × (–0,3) = –0,027.

(0,3)³ = (0,3) × (0,3) × (0,3) = 0,027.

g. Nyatakan perpangkatan (–2)³ dan (–2)⁴ dalam bentuk bilangan biasa.

(–2)³ = (–2) × (–2) × (–2) = –8.

(–2)⁴ = (–2) × (–2) × (–2) × (–2) = 16.

h. 3 + 2 × 5².

3 + 2 × 5² = 3 + 2 × 25 (Hitung hasil perpangkatan).

= 3 + 50 (Lakukan operasi perkalian).

= 53.

i. 4³ : 8 + 3².

4³ : 8 + 3² = 64 : 8 + 9 (Hitung hasil tiap-tiap perpangkatan).

= 8 + 9 (Lakukan operasi pembagian dulu).

= 17.

Itulah definisi atau pengertian bilangan berpangkat dan contoh soalnya. Semangat belajar ya. (Z-2)