Rumus Matriks: Dasar-Dasar untuk Pemula dalam Matematika

MATRIKS, sebuah konsep fundamental dalam matematika, seringkali dianggap menakutkan bagi pemula. Padahal, dengan pemahaman yang tepat, matriks dapat menjadi alat yang sangat berguna dalam berbagai bidang, mulai dari ilmu komputer hingga ekonomi. Artikel ini akan mengupas tuntas dasar-dasar matriks, membimbing Anda langkah demi langkah untuk memahami konsep ini dengan mudah dan menyenangkan.

Apa Itu Matriks?

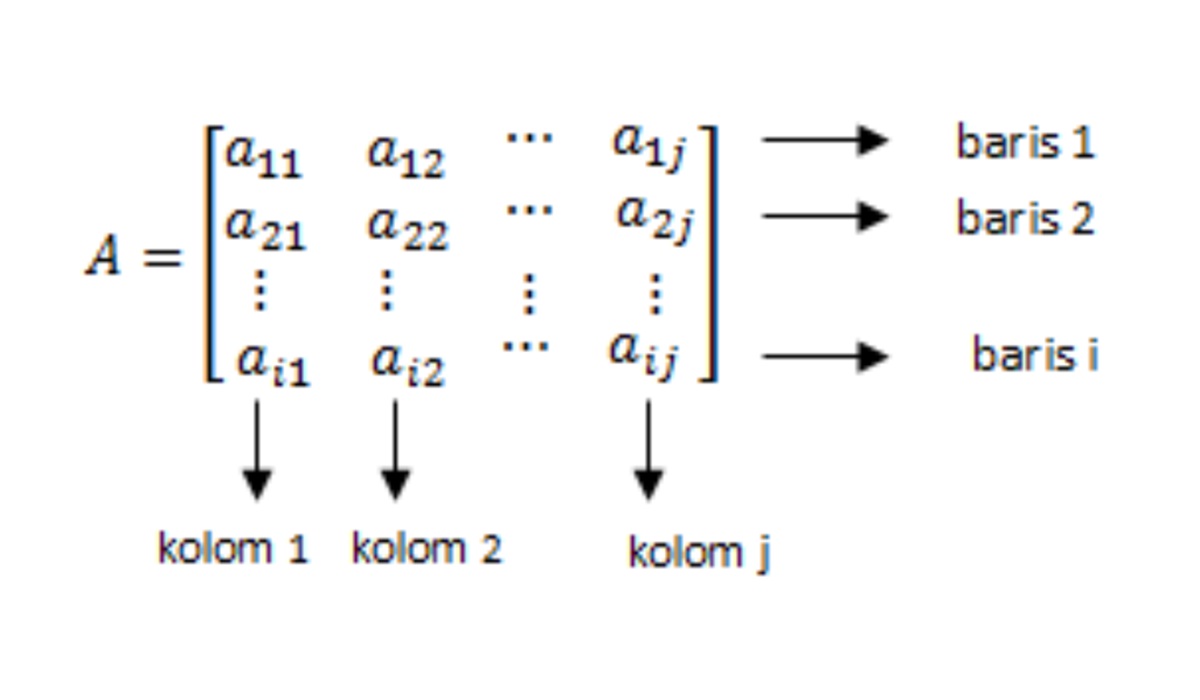
Secara sederhana, matriks adalah susunan bilangan yang diatur dalam baris dan kolom. Bayangkan sebuah tabel angka; itulah representasi visual dari matriks. Setiap angka dalam matriks disebut elemen atau entri. Ukuran matriks ditentukan oleh jumlah baris dan kolomnya. Misalnya, matriks dengan 3 baris dan 2 kolom disebut matriks 3x2 (dibaca tiga kali dua).

Notasi matriks biasanya menggunakan huruf kapital, misalnya A, B, atau C. Elemen-elemen matriks diidentifikasi dengan menggunakan indeks baris dan kolom. Misalnya, elemen pada baris ke-i dan kolom ke-j dari matriks A dinotasikan sebagai a_ij.

Baca juga : Simbol Matematika: Definisi dan Contoh Penggunaan

Contoh:

Matriks A = 1 2 3 4 5 6

Matriks A adalah matriks 3x2. Elemen a₁₁ (baris 1, kolom 1) adalah 1, elemen a₂₂ (baris 2, kolom 2) adalah 4, dan seterusnya.

Baca juga : Persamaan Kuadrat: Rumus dan Contoh Penyelesaian

Jenis-Jenis Matriks

Terdapat berbagai jenis matriks dengan karakteristik khusus:

• Matriks Persegi: Matriks dengan jumlah baris dan kolom yang sama (n x n).
• Matriks Baris: Matriks hanya dengan satu baris (1 x n).
• Matriks Kolom: Matriks hanya dengan satu kolom (n x 1).
• Matriks Nol: Matriks yang semua elemennya bernilai nol.
• Matriks Identitas: Matriks persegi yang elemen diagonal utamanya bernilai 1, dan elemen lainnya bernilai 0. Matriks identitas dinotasikan dengan I.
• Matriks Diagonal: Matriks persegi yang semua elemen di luar diagonal utamanya bernilai 0.
• Matriks Segitiga Atas: Matriks persegi yang semua elemen di bawah diagonal utamanya bernilai 0.
• Matriks Segitiga Bawah: Matriks persegi yang semua elemen di atas diagonal utamanya bernilai 0.
• Matriks Transpose: Matriks yang diperoleh dengan menukar baris dan kolom matriks asli. Transpose dari matriks A dinotasikan dengan A^T.

Operasi pada Matriks

Matriks dapat dioperasikan dengan berbagai cara, termasuk penjumlahan, pengurangan, perkalian skalar, dan perkalian matriks.

Penjumlahan dan Pengurangan Matriks

Penjumlahan dan pengurangan matriks hanya dapat dilakukan jika matriks-matriks tersebut memiliki ukuran yang sama. Operasi ini dilakukan dengan menjumlahkan atau mengurangkan elemen-elemen yang bersesuaian.

Baca juga : Rumus Matriks: Dasar-Dasar dan Contoh Penggunaan

Misalnya, jika A dan B adalah matriks m x n, maka:

(A + B)_ij = A_ij + B_ij

(A - B)_ij = A_ij - B_ij

Baca juga : Luas Belah Ketupat: Rumus dan Contoh Soal Mudah

Contoh:

A = 1 2 3 4

B = 5 6 7 8

A + B = 6 8 10 12

A - B = -4 -4 -4 -4

Perkalian Skalar

Perkalian skalar adalah operasi mengalikan matriks dengan sebuah bilangan (skalar). Operasi ini dilakukan dengan mengalikan setiap elemen matriks dengan skalar tersebut.

Misalnya, jika A adalah matriks m x n dan k adalah skalar, maka:

(kA)_ij = k A_ij

Contoh:

A = 1 2 3 4

k = 2

kA = 2 4 6 8

Perkalian Matriks

Perkalian matriks lebih kompleks daripada operasi lainnya. Dua matriks, A dan B, dapat dikalikan jika jumlah kolom matriks A sama dengan jumlah baris matriks B. Jika A adalah matriks m x n dan B adalah matriks n x p, maka hasil perkalian AB adalah matriks m x p.

Elemen (AB)_ij dihitung dengan menjumlahkan hasil perkalian elemen-elemen pada baris ke-i dari matriks A dengan elemen-elemen pada kolom ke-j dari matriks B.

(AB)_ij = A_i1B_1j + A_i2B_2j + ... + A_inB_nj

Contoh:

A = 1 2 3 4

B = 5 6 7 8

AB = (15 + 27) (16 + 28) (35 + 47) (36 + 48)

AB = 19 22 43 50

Penting: Perkalian matriks tidak komutatif, artinya AB tidak selalu sama dengan BA.

Determinan Matriks

Determinan adalah nilai skalar yang dapat dihitung dari matriks persegi. Determinan memberikan informasi penting tentang matriks, seperti apakah matriks tersebut invertible (memiliki invers) atau tidak.

Determinan Matriks 2x2

Untuk matriks 2x2, determinan dihitung sebagai berikut:

A = a b c d

det(A) = ad - bc

Contoh:

A = 1 2 3 4

det(A) = (14) - (23) = 4 - 6 = -2

Determinan Matriks 3x3

Untuk matriks 3x3, determinan dapat dihitung menggunakan berbagai metode, salah satunya adalah metode Sarrus:

A = a b c d e f g h i

det(A) = aei + bfg + cdh - ceg - bdi - afh

Contoh:

A = 1 2 3 4 5 6 7 8 9

det(A) = (159) + (267) + (348) - (357) - (249) - (168) = 45 + 84 + 96 - 105 - 72 - 48 = 0

Untuk matriks yang lebih besar dari 3x3, perhitungan determinan menjadi lebih kompleks dan biasanya dilakukan dengan menggunakan metode ekspansi kofaktor atau reduksi baris.

Invers Matriks

Invers matriks adalah matriks yang, ketika dikalikan dengan matriks asli, menghasilkan matriks identitas. Tidak semua matriks memiliki invers. Matriks yang memiliki invers disebut matriks invertible atau nonsingular, sedangkan matriks yang tidak memiliki invers disebut matriks singular.

Invers Matriks 2x2

Untuk matriks 2x2, invers dapat dihitung sebagai berikut:

A = a b c d

A^-1 = (1/det(A)) d -b -c a

Catatan: Matriks A hanya memiliki invers jika determinannya tidak sama dengan nol.

Contoh:

A = 1 2 3 4

det(A) = -2 (seperti yang dihitung sebelumnya)

A^-1 = (1/-2) 4 -2 -3 1

A^-1 = -2 1 1.5 -0.5

Untuk matriks yang lebih besar dari 2x2, perhitungan invers matriks menjadi lebih kompleks dan biasanya dilakukan dengan menggunakan metode adjoin atau eliminasi Gauss-Jordan.

Aplikasi Matriks

Matriks memiliki banyak aplikasi dalam berbagai bidang, di antaranya:

• Grafika Komputer: Matriks digunakan untuk transformasi objek 3D, seperti rotasi, translasi, dan penskalaan.
• Ilmu Komputer: Matriks digunakan dalam algoritma machine learning, pengolahan citra, dan analisis data.
• Fisika: Matriks digunakan untuk merepresentasikan transformasi linear, seperti rotasi dan refleksi, serta dalam mekanika kuantum.
• Ekonomi: Matriks digunakan untuk memodelkan sistem ekonomi, menganalisis data pasar, dan mengoptimalkan investasi.
• Teknik: Matriks digunakan dalam analisis struktur, kontrol sistem, dan pemrosesan sinyal.
• Kriptografi: Matriks digunakan dalam beberapa algoritma enkripsi untuk mengamankan data.

Contoh Soal dan Pembahasan

Berikut adalah beberapa contoh soal tentang matriks beserta pembahasannya:

Soal 1:

Diberikan matriks A = 2 1 0 3

dan B = -1 2 4 1

Hitunglah A + B.

Pembahasan:

A + B = (2 + (-1)) (1 + 2) (0 + 4) (3 + 1)

A + B = 1 3 4 4

Soal 2:

Diberikan matriks A = 1 2 3 4

Hitunglah 2A.

Pembahasan:

2A = (21) (22) (23) (24)

2A = 2 4 6 8

Soal 3:

Diberikan matriks A = 1 2 3 4

dan B = 5 6 7 8

Hitunglah AB.

Pembahasan:

AB = (15 + 27) (16 + 28) (35 + 47) (36 + 48)

AB = 19 22 43 50

Soal 4:

Diberikan matriks A = 2 3 1 4

Hitunglah determinan dari A.

Pembahasan:

det(A) = (24) - (31) = 8 - 3 = 5

Soal 5:

Diberikan matriks A = 1 2 3 4

Hitunglah invers dari A.

Pembahasan:

det(A) = (14) - (23) = -2

A^-1 = (1/-2) 4 -2 -3 1

A^-1 = -2 1 1.5 -0.5

Tips dan Trik dalam Mempelajari Matriks

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam mempelajari matriks:

• Pahami Konsep Dasar: Pastikan Anda memahami definisi matriks, jenis-jenis matriks, dan operasi-operasi dasar pada matriks.
• Latihan Soal: Kerjakan banyak soal latihan untuk mengasah kemampuan Anda dalam menerapkan konsep-konsep matriks.
• Gunakan Alat Bantu: Manfaatkan kalkulator matriks atau perangkat lunak matematika untuk membantu Anda dalam perhitungan yang kompleks.
• Visualisasikan Matriks: Bayangkan matriks sebagai tabel angka atau representasi visual lainnya untuk mempermudah pemahaman.
• Cari Sumber Belajar Tambahan: Baca buku, artikel, atau tonton video tutorial tentang matriks untuk memperluas pengetahuan Anda.
• Berkolaborasi dengan Teman: Diskusikan konsep-konsep matriks dengan teman atau guru untuk mendapatkan perspektif yang berbeda.
• Jangan Menyerah: Matriks mungkin terasa sulit pada awalnya, tetapi dengan ketekunan dan latihan yang cukup, Anda pasti bisa menguasainya.

Kesimpulan

Matriks adalah konsep penting dalam matematika dengan banyak aplikasi dalam berbagai bidang. Dengan memahami dasar-dasar matriks, Anda akan memiliki alat yang berguna untuk memecahkan masalah yang kompleks dan mengembangkan pemahaman yang lebih dalam tentang dunia di sekitar Anda. Jangan takut untuk menjelajahi lebih jauh tentang matriks dan aplikasinya, karena pengetahuan ini akan sangat bermanfaat bagi Anda di masa depan.

Selamat belajar dan semoga sukses!