Rumus Pecahan: Menghitung Bagian dalam Matematika

Pecahan, sebuah konsep fundamental dalam matematika, merepresentasikan bagian dari keseluruhan. Memahami dan menguasai operasi pecahan adalah kunci untuk membuka berbagai bidang matematika lainnya, mulai dari aljabar hingga kalkulus. Lebih dari sekadar angka, pecahan adalah alat yang ampuh untuk memecahkan masalah sehari-hari, mulai dari membagi pizza hingga menghitung proporsi dalam resep masakan.

Memahami Esensi Pecahan

Secara sederhana, pecahan terdiri dari dua bagian utama: pembilang dan penyebut. Pembilang menunjukkan berapa banyak bagian yang kita miliki, sedangkan penyebut menunjukkan berapa banyak bagian yang membentuk keseluruhan. Misalnya, dalam pecahan 3/4, angka 3 adalah pembilang dan angka 4 adalah penyebut. Ini berarti kita memiliki 3 bagian dari keseluruhan yang dibagi menjadi 4 bagian yang sama.

Penting untuk diingat bahwa penyebut tidak boleh sama dengan nol. Jika penyebut adalah nol, maka pecahan tersebut tidak terdefinisi. Hal ini karena kita tidak dapat membagi sesuatu menjadi nol bagian.

Selain pembilang dan penyebut, ada beberapa jenis pecahan yang perlu kita ketahui:

• Pecahan Biasa: Pecahan yang pembilangnya lebih kecil dari penyebut. Contoh: 1/2, 2/3, 3/4.
• Pecahan Tidak Biasa: Pecahan yang pembilangnya lebih besar atau sama dengan penyebut. Contoh: 5/4, 7/3, 4/4.
• Pecahan Campuran: Kombinasi bilangan bulat dan pecahan biasa. Contoh: 1 1/2, 2 1/4, 3 2/5.
• Pecahan Desimal: Representasi pecahan dalam bentuk desimal. Contoh: 0.5, 0.75, 0.25.

Setiap jenis pecahan memiliki karakteristik dan kegunaannya masing-masing. Memahami perbedaan di antara mereka akan membantu kita dalam menyelesaikan berbagai masalah matematika.

Operasi Dasar pada Pecahan

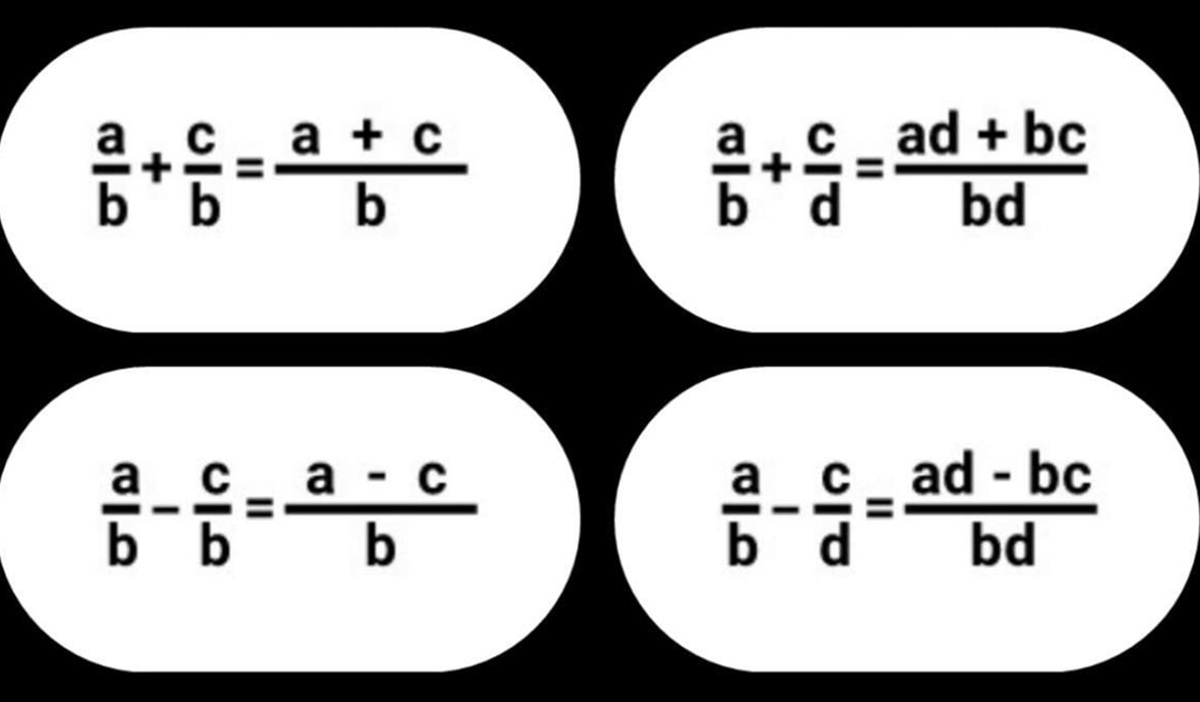
Seperti bilangan bulat, pecahan juga dapat dioperasikan dengan operasi dasar matematika seperti penjumlahan, pengurangan, perkalian, dan pembagian. Namun, ada beberapa aturan khusus yang perlu diperhatikan saat melakukan operasi pada pecahan.

Penjumlahan dan Pengurangan Pecahan

Untuk menjumlahkan atau mengurangkan pecahan, kita perlu memastikan bahwa penyebutnya sama. Jika penyebutnya berbeda, kita perlu mencari kelipatan persekutuan terkecil (KPK) dari penyebut tersebut dan mengubah pecahan agar memiliki penyebut yang sama. Setelah penyebutnya sama, kita dapat menjumlahkan atau mengurangkan pembilangnya saja.

Contoh:

1/4 + 2/4 = (1+2)/4 = 3/4

3/5 - 1/5 = (3-1)/5 = 2/5

Jika penyebutnya berbeda:

1/2 + 1/3 = (3/6) + (2/6) = 5/6 (KPK dari 2 dan 3 adalah 6)

2/3 - 1/4 = (8/12) - (3/12) = 5/12 (KPK dari 3 dan 4 adalah 12)

Perkalian Pecahan

Perkalian pecahan adalah operasi yang paling sederhana. Kita hanya perlu mengalikan pembilang dengan pembilang dan penyebut dengan penyebut.

Contoh:

1/2 x 2/3 = (1x2)/(2x3) = 2/6 = 1/3 (disederhanakan)

3/4 x 1/5 = (3x1)/(4x5) = 3/20

Pembagian Pecahan

Pembagian pecahan melibatkan proses yang sedikit berbeda. Untuk membagi pecahan, kita perlu membalikkan pecahan kedua (pembagi) dan mengalikannya dengan pecahan pertama (yang dibagi).

Contoh:

1/2 : 2/3 = 1/2 x 3/2 = (1x3)/(2x2) = 3/4

3/4 : 1/5 = 3/4 x 5/1 = (3x5)/(4x1) = 15/4 = 3 3/4 (diubah menjadi pecahan campuran)

Penyederhanaan Pecahan

Setelah melakukan operasi pada pecahan, penting untuk menyederhanakannya ke bentuk yang paling sederhana. Pecahan dikatakan sederhana jika pembilang dan penyebut tidak memiliki faktor persekutuan selain 1. Untuk menyederhanakan pecahan, kita perlu mencari faktor persekutuan terbesar (FPB) dari pembilang dan penyebut, lalu membagi keduanya dengan FPB tersebut.

Contoh:

4/6 dapat disederhanakan menjadi 2/3 (FPB dari 4 dan 6 adalah 2)

12/18 dapat disederhanakan menjadi 2/3 (FPB dari 12 dan 18 adalah 6)

Penyederhanaan pecahan memudahkan kita untuk memahami nilai pecahan dan membandingkannya dengan pecahan lainnya.

Mengubah Pecahan ke Bentuk Desimal dan Sebaliknya

Pecahan dapat diubah menjadi bentuk desimal dengan cara membagi pembilang dengan penyebut. Hasilnya adalah bilangan desimal yang mungkin berulang atau tidak berulang.

Contoh:

1/2 = 0.5

1/3 = 0.333...

1/4 = 0.25

Sebaliknya, bilangan desimal dapat diubah menjadi pecahan dengan cara menuliskan bilangan desimal tersebut sebagai pecahan dengan penyebut 10, 100, 1000, dan seterusnya, tergantung pada jumlah angka di belakang koma. Kemudian, pecahan tersebut disederhanakan.

Contoh:

0.5 = 5/10 = 1/2

0.25 = 25/100 = 1/4

0.75 = 75/100 = 3/4

Penerapan Pecahan dalam Kehidupan Sehari-hari

Pecahan bukan hanya konsep abstrak dalam matematika, tetapi juga memiliki banyak penerapan dalam kehidupan sehari-hari. Berikut adalah beberapa contoh:

• Memasak: Resep masakan sering menggunakan pecahan untuk menunjukkan jumlah bahan yang dibutuhkan. Misalnya, 1/2 sendok teh garam, 1/4 cangkir gula, dan sebagainya.
• Mengukur: Pecahan digunakan dalam pengukuran panjang, berat, dan volume. Misalnya, 1/2 meter kain, 1/4 kilogram tepung, dan sebagainya.
• Keuangan: Pecahan digunakan dalam perhitungan bunga, diskon, dan pajak. Misalnya, diskon 25% (1/4 dari harga awal), bunga 5% per tahun (5/100 dari modal awal), dan sebagainya.
• Waktu: Pecahan digunakan untuk menyatakan bagian dari jam atau menit. Misalnya, 1/2 jam (30 menit), 1/4 jam (15 menit), dan sebagainya.
• Probabilitas: Pecahan digunakan untuk menyatakan peluang suatu kejadian. Misalnya, peluang mendapatkan angka 6 saat melempar dadu adalah 1/6.

Dengan memahami konsep pecahan, kita dapat menyelesaikan berbagai masalah praktis dalam kehidupan sehari-hari dengan lebih mudah dan efisien.

Tips dan Trik dalam Menyelesaikan Soal Pecahan

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam menyelesaikan soal pecahan:

• Pahami konsep dasar: Pastikan Anda memahami konsep dasar pecahan, seperti pembilang, penyebut, jenis-jenis pecahan, dan operasi dasar pada pecahan.
• Latihan secara teratur: Semakin sering Anda berlatih, semakin mahir Anda dalam menyelesaikan soal pecahan.
• Gunakan alat bantu: Jika Anda kesulitan, gunakan alat bantu seperti garis bilangan atau diagram untuk memvisualisasikan pecahan.
• Periksa jawaban Anda: Setelah menyelesaikan soal, periksa kembali jawaban Anda untuk memastikan tidak ada kesalahan.
• Sederhanakan pecahan: Selalu sederhanakan pecahan ke bentuk yang paling sederhana setelah melakukan operasi.
• Ubah pecahan ke bentuk desimal atau sebaliknya: Jika soal melibatkan pecahan dan bilangan desimal, ubah keduanya ke bentuk yang sama agar lebih mudah dioperasikan.
• Gunakan kalkulator: Jika soal terlalu rumit, gunakan kalkulator untuk membantu Anda menghitung. Namun, pastikan Anda memahami konsep dasarnya terlebih dahulu.
• Kerjakan soal secara sistematis: Ikuti langkah-langkah yang jelas dan terstruktur saat menyelesaikan soal pecahan.
• Jangan menyerah: Jika Anda mengalami kesulitan, jangan menyerah. Coba lagi dan lagi sampai Anda berhasil.
• Minta bantuan: Jika Anda benar-benar kesulitan, jangan ragu untuk meminta bantuan dari guru, teman, atau tutor.

Kesalahan Umum dalam Mengerjakan Soal Pecahan

Berikut adalah beberapa kesalahan umum yang sering dilakukan saat mengerjakan soal pecahan:

• Tidak menyamakan penyebut saat menjumlahkan atau mengurangkan pecahan.
• Salah membalikkan pecahan saat membagi pecahan.
• Tidak menyederhanakan pecahan ke bentuk yang paling sederhana.
• Salah mengubah pecahan ke bentuk desimal atau sebaliknya.
• Tidak memahami konsep dasar pecahan.
• Terburu-buru dalam mengerjakan soal.
• Tidak memeriksa jawaban.

Dengan menghindari kesalahan-kesalahan ini, Anda dapat meningkatkan kemampuan Anda dalam menyelesaikan soal pecahan.

Pecahan dalam Konteks yang Lebih Luas

Pecahan adalah fondasi bagi konsep matematika yang lebih kompleks. Pemahaman yang kuat tentang pecahan akan membantu Anda dalam mempelajari aljabar, kalkulus, dan bidang matematika lainnya. Selain itu, pecahan juga penting dalam berbagai bidang ilmu pengetahuan dan teknologi, seperti fisika, kimia, teknik, dan ilmu komputer.

Dalam aljabar, pecahan digunakan untuk menyatakan variabel dan koefisien. Dalam kalkulus, pecahan digunakan untuk menghitung turunan dan integral. Dalam fisika, pecahan digunakan untuk menyatakan kecepatan, percepatan, dan gaya. Dalam kimia, pecahan digunakan untuk menyatakan konsentrasi larutan. Dalam teknik, pecahan digunakan untuk merancang struktur dan sistem. Dalam ilmu komputer, pecahan digunakan untuk merepresentasikan data dan algoritma.

Oleh karena itu, menguasai konsep pecahan adalah investasi yang berharga untuk masa depan Anda.

Sumber Daya Tambahan untuk Mempelajari Pecahan

Jika Anda ingin mempelajari lebih lanjut tentang pecahan, berikut adalah beberapa sumber daya tambahan yang dapat Anda manfaatkan:

• Buku teks matematika: Buku teks matematika adalah sumber daya yang komprehensif untuk mempelajari pecahan.
• Situs web matematika: Ada banyak situs web matematika yang menawarkan pelajaran, latihan, dan soal-soal pecahan.
• Video tutorial matematika: Video tutorial matematika dapat membantu Anda memahami konsep pecahan secara visual.
• Aplikasi matematika: Ada banyak aplikasi matematika yang menawarkan latihan dan soal-soal pecahan.
• Guru atau tutor matematika: Jika Anda membutuhkan bantuan tambahan, Anda dapat meminta bantuan dari guru atau tutor matematika.

Dengan memanfaatkan sumber daya ini, Anda dapat meningkatkan pemahaman Anda tentang pecahan dan menjadi lebih mahir dalam menyelesaikan soal pecahan.

Kesimpulan

Pecahan adalah konsep fundamental dalam matematika yang memiliki banyak penerapan dalam kehidupan sehari-hari. Dengan memahami konsep dasar pecahan, operasi dasar pada pecahan, dan tips dan trik dalam menyelesaikan soal pecahan, Anda dapat meningkatkan kemampuan Anda dalam matematika dan menyelesaikan berbagai masalah praktis dengan lebih mudah dan efisien. Jangan lupa untuk terus berlatih dan memanfaatkan sumber daya yang tersedia untuk meningkatkan pemahaman Anda tentang pecahan.

Selamat belajar dan semoga sukses! (Z-2)