Rumus Limas: Memahami Geometri dengan Mudah

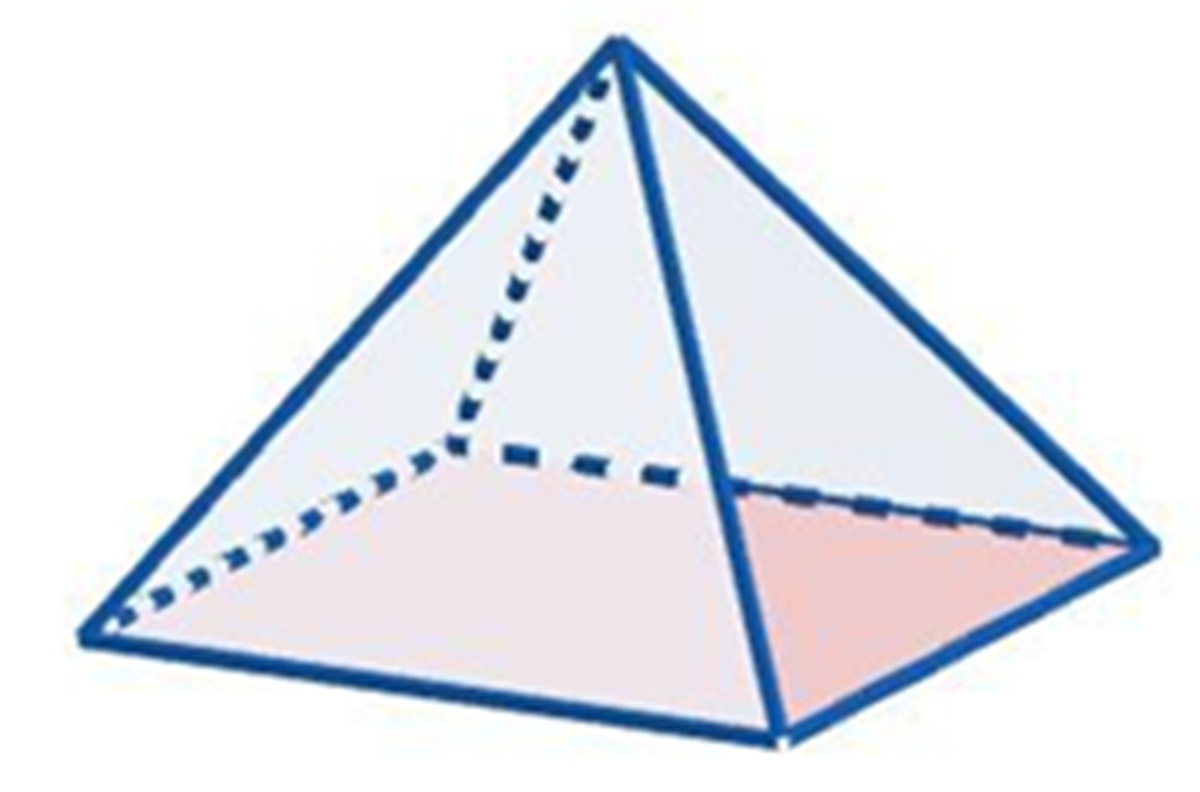
Limas, sebuah bangun ruang yang memikat dengan keindahan geometrisnya, seringkali menjadi tantangan tersendiri bagi sebagian orang. Bentuknya yang khas, dengan alas berupa poligon dan sisi-sisi tegak berbentuk segitiga yang bertemu pada satu titik puncak, menjadikannya objek yang menarik untuk dipelajari. Namun, di balik keindahannya, tersembunyi rumus-rumus yang perlu dipahami agar kita dapat menghitung berbagai propertinya, seperti luas permukaan dan volume. Mari kita telaah lebih dalam mengenai rumus limas dan bagaimana cara mengaplikasikannya dalam berbagai situasi.

Memahami Komponen Limas

Sebelum kita membahas rumus-rumus yang berkaitan dengan limas, penting untuk memahami terlebih dahulu komponen-komponen yang menyusun bangun ruang ini. Komponen-komponen tersebut meliputi:

• Alas: Alas limas adalah bidang poligon yang menjadi dasar dari bangun ruang ini. Bentuk alas dapat bervariasi, mulai dari segitiga, segiempat, segilima, hingga poligon dengan jumlah sisi yang lebih banyak.
• Sisi Tegak: Sisi tegak limas adalah bidang-bidang segitiga yang menghubungkan alas dengan titik puncak. Jumlah sisi tegak limas sama dengan jumlah sisi pada alas.
• Titik Puncak: Titik puncak adalah titik pertemuan dari semua sisi tegak limas.
• Tinggi Limas: Tinggi limas adalah jarak tegak lurus dari titik puncak ke bidang alas.
• Rusuk Alas: Rusuk alas adalah garis yang menjadi sisi dari poligon alas.
• Rusuk Tegak: Rusuk tegak adalah garis yang menghubungkan titik puncak dengan setiap sudut pada alas.

Dengan memahami komponen-komponen ini, kita akan lebih mudah dalam memahami rumus-rumus yang akan kita bahas selanjutnya.

Baca juga : Persamaan Kuadrat: Rumus dan Contoh Penyelesaian

Rumus Luas Permukaan Limas

Luas permukaan limas adalah jumlah luas seluruh bidang yang membentuk limas tersebut. Ini terdiri dari luas alas dan luas seluruh sisi tegaknya. Secara matematis, rumus luas permukaan limas dapat dituliskan sebagai berikut:

Luas Permukaan = Luas Alas + Jumlah Luas Sisi Tegak

Rumus ini berlaku untuk semua jenis limas, baik limas segitiga, limas segiempat, maupun limas dengan alas berbentuk poligon lainnya. Namun, untuk menghitung luas alas dan luas sisi tegak, kita perlu menyesuaikan dengan bentuk alas dan sisi tegak limas tersebut.

Baca juga : Volume Limas: Rumus dan Contohnya dalam Soal Matematika

Luas Alas Limas

Luas alas limas tergantung pada bentuk alasnya. Berikut adalah beberapa rumus luas alas untuk beberapa bentuk alas yang umum:

• Alas Segitiga: Luas alas segitiga dapat dihitung dengan rumus: Luas = 1/2 alas tinggi, di mana alas dan tinggi adalah alas dan tinggi segitiga.
• Alas Segiempat: Luas alas segiempat dapat dihitung dengan rumus: Luas = panjang lebar, jika alasnya berbentuk persegi panjang, atau Luas = sisi sisi, jika alasnya berbentuk persegi.
• Alas Segilima: Luas alas segilima dapat dihitung dengan rumus yang lebih kompleks, tergantung pada jenis segilima tersebut (segilima beraturan atau tidak beraturan). Untuk segilima beraturan, rumus yang digunakan adalah: Luas = (5/4) s^2 cot(π/5), di mana s adalah panjang sisi segilima.
• Alas Segienam: Luas alas segienam beraturan dapat dihitung dengan rumus: Luas = (3√3/2) s^2, di mana s adalah panjang sisi segienam.

Untuk alas berbentuk poligon lainnya, kita perlu menggunakan rumus yang sesuai dengan bentuk poligon tersebut.

Luas Sisi Tegak Limas

Sisi tegak limas selalu berbentuk segitiga. Oleh karena itu, untuk menghitung luas sisi tegak, kita menggunakan rumus luas segitiga, yaitu: Luas = 1/2 alas tinggi. Dalam konteks limas, alas segitiga adalah rusuk alas limas, dan tinggi segitiga adalah tinggi sisi tegak limas (sering disebut juga sebagai apotema limas).

Baca juga : Menghitung Volume Limas: Rumus dan Contoh Soal

Jika limas memiliki alas berbentuk poligon beraturan, maka semua sisi tegaknya akan memiliki luas yang sama. Dalam kasus ini, kita cukup menghitung luas salah satu sisi tegak, kemudian mengalikannya dengan jumlah sisi tegak (yang sama dengan jumlah sisi alas).

Namun, jika limas memiliki alas berbentuk poligon tidak beraturan, maka kita perlu menghitung luas setiap sisi tegak secara terpisah, karena masing-masing sisi tegak mungkin memiliki ukuran yang berbeda.

Rumus Volume Limas

Volume limas adalah ukuran ruang yang ditempati oleh limas tersebut. Rumus volume limas adalah sebagai berikut:

Baca juga : Menghitung Volume Limas: Rumus dan Contoh Soal

Volume = 1/3 Luas Alas Tinggi Limas

Rumus ini berlaku untuk semua jenis limas, tanpa memandang bentuk alasnya. Yang perlu diperhatikan adalah, tinggi limas yang digunakan dalam rumus ini adalah tinggi tegak lurus dari titik puncak ke bidang alas.

Untuk menghitung volume limas, kita perlu mengetahui luas alas dan tinggi limas. Luas alas dapat dihitung dengan rumus yang sesuai dengan bentuk alasnya, seperti yang telah dijelaskan sebelumnya. Tinggi limas biasanya diberikan dalam soal, atau dapat dihitung menggunakan teorema Pythagoras jika kita mengetahui panjang rusuk tegak dan jarak dari titik puncak ke salah satu sudut alas.

Contoh Soal dan Pembahasan

Untuk memperjelas pemahaman kita mengenai rumus limas, mari kita bahas beberapa contoh soal berikut:

Contoh Soal 1:

Sebuah limas segiempat memiliki alas berbentuk persegi dengan panjang sisi 8 cm. Tinggi limas adalah 12 cm. Hitunglah luas permukaan dan volume limas tersebut.

Pembahasan:

Luas Permukaan:

• Luas Alas = sisi sisi = 8 cm 8 cm = 64 cm²
• Untuk menghitung luas sisi tegak, kita perlu mencari tinggi sisi tegak (apotema). Kita dapat menggunakan teorema Pythagoras untuk mencari apotema. Misalkan apotema adalah 'a'. Maka, a² = (sisi/2)² + tinggi² = (8/2)² + 12² = 4² + 12² = 16 + 144 = 160. Jadi, a = √160 ≈ 12.65 cm
• Luas Satu Sisi Tegak = 1/2 alas tinggi = 1/2 8 cm 12.65 cm ≈ 50.6 cm²
• Jumlah Luas Sisi Tegak = 4 50.6 cm² ≈ 202.4 cm²
• Luas Permukaan = Luas Alas + Jumlah Luas Sisi Tegak = 64 cm² + 202.4 cm² ≈ 266.4 cm²

Volume:

• Volume = 1/3 Luas Alas Tinggi Limas = 1/3 64 cm² 12 cm = 256 cm³

Jadi, luas permukaan limas tersebut adalah sekitar 266.4 cm², dan volumenya adalah 256 cm³.

Contoh Soal 2:

Sebuah limas segitiga memiliki alas berbentuk segitiga sama sisi dengan panjang sisi 6 cm. Tinggi limas adalah 10 cm. Hitunglah volume limas tersebut.

Pembahasan:

• Luas Alas (Segitiga Sama Sisi) = (√3/4) sisi² = (√3/4) 6² = (√3/4) 36 ≈ 15.59 cm²
• Volume = 1/3 Luas Alas Tinggi Limas = 1/3 15.59 cm² 10 cm ≈ 51.97 cm³

Jadi, volume limas tersebut adalah sekitar 51.97 cm³.

Jenis-Jenis Limas

Limas dapat diklasifikasikan berdasarkan bentuk alasnya. Berikut adalah beberapa jenis limas yang umum:

• Limas Segitiga: Limas yang alasnya berbentuk segitiga. Limas segitiga juga dikenal sebagai tetrahedron.
• Limas Segiempat: Limas yang alasnya berbentuk segiempat (persegi, persegi panjang, trapesium, dll.).
• Limas Segilima: Limas yang alasnya berbentuk segilima.
• Limas Segienam: Limas yang alasnya berbentuk segienam.
• Limas Beraturan: Limas yang alasnya berbentuk poligon beraturan (semua sisi dan sudutnya sama). Pada limas beraturan, semua sisi tegaknya kongruen (memiliki ukuran dan bentuk yang sama).
• Limas Tidak Beraturan: Limas yang alasnya berbentuk poligon tidak beraturan. Pada limas tidak beraturan, sisi-sisi tegaknya mungkin memiliki ukuran dan bentuk yang berbeda.

Selain berdasarkan bentuk alasnya, limas juga dapat diklasifikasikan berdasarkan posisi titik puncaknya terhadap alas:

• Limas Tegak: Limas yang titik puncaknya berada tepat di atas pusat alas. Dengan kata lain, tinggi limas tegak lurus dengan bidang alas.
• Limas Miring: Limas yang titik puncaknya tidak berada tepat di atas pusat alas. Akibatnya, tinggi limas tidak tegak lurus dengan bidang alas.

Aplikasi Rumus Limas dalam Kehidupan Sehari-hari

Rumus limas tidak hanya berguna dalam pelajaran matematika di sekolah, tetapi juga memiliki aplikasi praktis dalam kehidupan sehari-hari. Berikut adalah beberapa contoh aplikasi rumus limas:

• Arsitektur: Bangunan-bangunan dengan atap berbentuk limas seringkali menggunakan rumus limas untuk menghitung volume ruang di dalam atap, serta luas permukaan atap untuk keperluan perhitungan material.
• Konstruksi: Dalam konstruksi jalan atau bendungan, rumus limas dapat digunakan untuk menghitung volume material yang dibutuhkan untuk membuat tumpukan material berbentuk limas.
• Desain Produk: Beberapa produk, seperti kemasan makanan atau hiasan rumah, memiliki bentuk limas. Rumus limas dapat digunakan untuk menghitung volume atau luas permukaan produk tersebut.
• Geologi: Dalam ilmu geologi, rumus limas dapat digunakan untuk memperkirakan volume gunung berapi atau bukit yang berbentuk limas.
• Pemodelan 3D: Dalam pemodelan 3D, limas sering digunakan sebagai bentuk dasar untuk membuat objek yang lebih kompleks. Pemahaman mengenai rumus limas akan membantu dalam membuat model 3D yang akurat.

Tips dan Trik dalam Mengerjakan Soal Limas

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam mengerjakan soal-soal yang berkaitan dengan limas:

• Pahami Konsep Dasar: Pastikan Anda memahami konsep dasar mengenai limas, termasuk komponen-komponennya (alas, sisi tegak, titik puncak, tinggi) dan jenis-jenis limas.
• Gambarkan Sketsa: Menggambar sketsa limas dapat membantu Anda memvisualisasikan soal dan memahami hubungan antara berbagai komponen limas.
• Identifikasi Informasi yang Diketahui: Baca soal dengan cermat dan identifikasi informasi yang diketahui (misalnya, panjang sisi alas, tinggi limas, luas alas).
• Pilih Rumus yang Tepat: Pilih rumus yang sesuai dengan jenis limas dan informasi yang diketahui. Pastikan Anda memahami arti dari setiap variabel dalam rumus tersebut.
• Perhatikan Satuan: Pastikan semua satuan yang digunakan dalam perhitungan adalah sama. Jika ada satuan yang berbeda, konversikan terlebih dahulu ke satuan yang sama.
• Gunakan Teorema Pythagoras: Teorema Pythagoras seringkali berguna dalam mencari tinggi sisi tegak (apotema) atau tinggi limas, terutama jika diberikan informasi mengenai panjang rusuk tegak dan jarak dari titik puncak ke salah satu sudut alas.
• Periksa Kembali Jawaban: Setelah mendapatkan jawaban, periksa kembali untuk memastikan bahwa jawaban tersebut masuk akal dan sesuai dengan soal.

Kesimpulan

Limas adalah bangun ruang yang menarik dengan berbagai aplikasi dalam kehidupan sehari-hari. Memahami rumus luas permukaan dan volume limas, serta komponen-komponen yang menyusunnya, akan membantu kita dalam menyelesaikan berbagai masalah yang berkaitan dengan limas. Dengan latihan yang cukup dan pemahaman yang mendalam, kita dapat menguasai geometri limas dengan mudah.

Semoga artikel ini bermanfaat bagi Anda dalam memahami rumus limas dan aplikasinya. Selamat belajar dan semoga sukses!