Sudut Siku-Siku: Pengertian dan Besarnya

Dalam dunia geometri yang kaya dan beragam, terdapat berbagai jenis sudut yang masing-masing memiliki karakteristik unik. Salah satu sudut yang paling mendasar dan sering ditemui adalah sudut siku-siku. Sudut ini menjadi fondasi penting dalam berbagai bidang, mulai dari matematika, arsitektur, hingga kehidupan sehari-hari. Pemahaman mendalam tentang sudut siku-siku akan membuka wawasan baru tentang bagaimana bentuk dan ruang saling berinteraksi.

Definisi dan Ukuran Sudut Siku-Siku

Sudut siku-siku secara sederhana dapat didefinisikan sebagai sudut yang besarnya tepat 90 derajat. Derajat merupakan satuan pengukuran sudut yang umum digunakan, di mana satu lingkaran penuh dibagi menjadi 360 derajat. Dengan demikian, sudut siku-siku mewakili seperempat dari lingkaran penuh. Sudut ini seringkali dilambangkan dengan simbol kotak kecil di titik sudutnya, yang membedakannya dari jenis sudut lainnya.

Keberadaan sudut siku-siku sangat penting karena menjadi acuan dasar untuk menentukan jenis sudut lainnya. Sudut yang lebih kecil dari 90 derajat disebut sudut lancip, sedangkan sudut yang lebih besar dari 90 derajat tetapi kurang dari 180 derajat disebut sudut tumpul. Sudut yang tepat 180 derajat disebut sudut lurus, dan sudut yang lebih besar dari 180 derajat tetapi kurang dari 360 derajat disebut sudut refleks.

Dalam trigonometri, sudut siku-siku memegang peranan krusial dalam definisi fungsi-fungsi trigonometri seperti sinus, kosinus, dan tangen. Fungsi-fungsi ini didefinisikan berdasarkan perbandingan sisi-sisi pada segitiga siku-siku, di mana salah satu sudutnya adalah sudut siku-siku. Segitiga siku-siku juga menjadi dasar dari teorema Pythagoras, yang menyatakan bahwa kuadrat sisi miring (sisi terpanjang) sama dengan jumlah kuadrat kedua sisi lainnya.

Karakteristik dan Sifat-Sifat Sudut Siku-Siku

Sudut siku-siku memiliki beberapa karakteristik dan sifat yang membedakannya dari jenis sudut lainnya. Salah satu sifat yang paling penting adalah bahwa dua garis yang membentuk sudut siku-siku dikatakan saling tegak lurus atau ortogonal. Artinya, kedua garis tersebut berpotongan pada sudut 90 derajat. Konsep tegak lurus ini sangat penting dalam berbagai aplikasi, seperti konstruksi bangunan, desain grafis, dan navigasi.

Selain itu, sudut siku-siku juga memiliki sifat reflektif. Jika sebuah cermin diletakkan pada garis yang membentuk sudut siku-siku, maka cahaya yang datang akan dipantulkan kembali pada arah yang berlawanan. Sifat ini dimanfaatkan dalam berbagai perangkat optik, seperti periskop dan reflektor.

Dalam geometri Euclidean, sudut siku-siku merupakan salah satu elemen dasar yang digunakan untuk membangun berbagai bentuk dan bangun datar. Persegi, persegi panjang, dan trapesium siku-siku adalah beberapa contoh bangun datar yang memiliki sudut siku-siku. Bangun-bangun ini seringkali digunakan dalam desain arsitektur, teknik sipil, dan manufaktur.

Penerapan Sudut Siku-Siku dalam Kehidupan Sehari-hari

Sudut siku-siku bukan hanya konsep abstrak dalam matematika, tetapi juga memiliki banyak penerapan praktis dalam kehidupan sehari-hari. Tanpa kita sadari, sudut siku-siku hadir di sekitar kita dalam berbagai bentuk dan fungsi. Berikut adalah beberapa contoh penerapan sudut siku-siku dalam kehidupan sehari-hari:

• Arsitektur dan Konstruksi: Sudut siku-siku sangat penting dalam desain dan konstruksi bangunan. Dinding, lantai, dan atap biasanya dibangun dengan sudut siku-siku untuk memastikan stabilitas dan kekuatan struktur. Pintu dan jendela juga seringkali dipasang dengan sudut siku-siku agar dapat dibuka dan ditutup dengan lancar.
• Pertukangan Kayu: Dalam pertukangan kayu, sudut siku-siku digunakan untuk membuat potongan kayu yang presisi dan akurat. Tukang kayu menggunakan alat seperti siku-siku untuk memastikan bahwa potongan kayu memiliki sudut 90 derajat, sehingga dapat dirakit menjadi struktur yang kokoh dan stabil.
• Desain Grafis: Dalam desain grafis, sudut siku-siku digunakan untuk membuat garis lurus, kotak, dan bentuk-bentuk geometris lainnya. Sudut siku-siku juga penting dalam mengatur tata letak elemen-elemen desain, seperti teks, gambar, dan logo.
• Navigasi: Dalam navigasi, sudut siku-siku digunakan untuk menentukan arah dan posisi. Kompas menggunakan sudut siku-siku untuk menunjukkan arah utara, selatan, timur, dan barat. Peta juga menggunakan sudut siku-siku untuk merepresentasikan jalan, sungai, dan batas-batas wilayah.
• Perangkat Rumah Tangga: Banyak perangkat rumah tangga yang menggunakan sudut siku-siku dalam desainnya. Contohnya, meja, kursi, lemari, dan rak biasanya memiliki sudut siku-siku untuk memastikan stabilitas dan fungsionalitas.

Cara Mengukur dan Membuat Sudut Siku-Siku

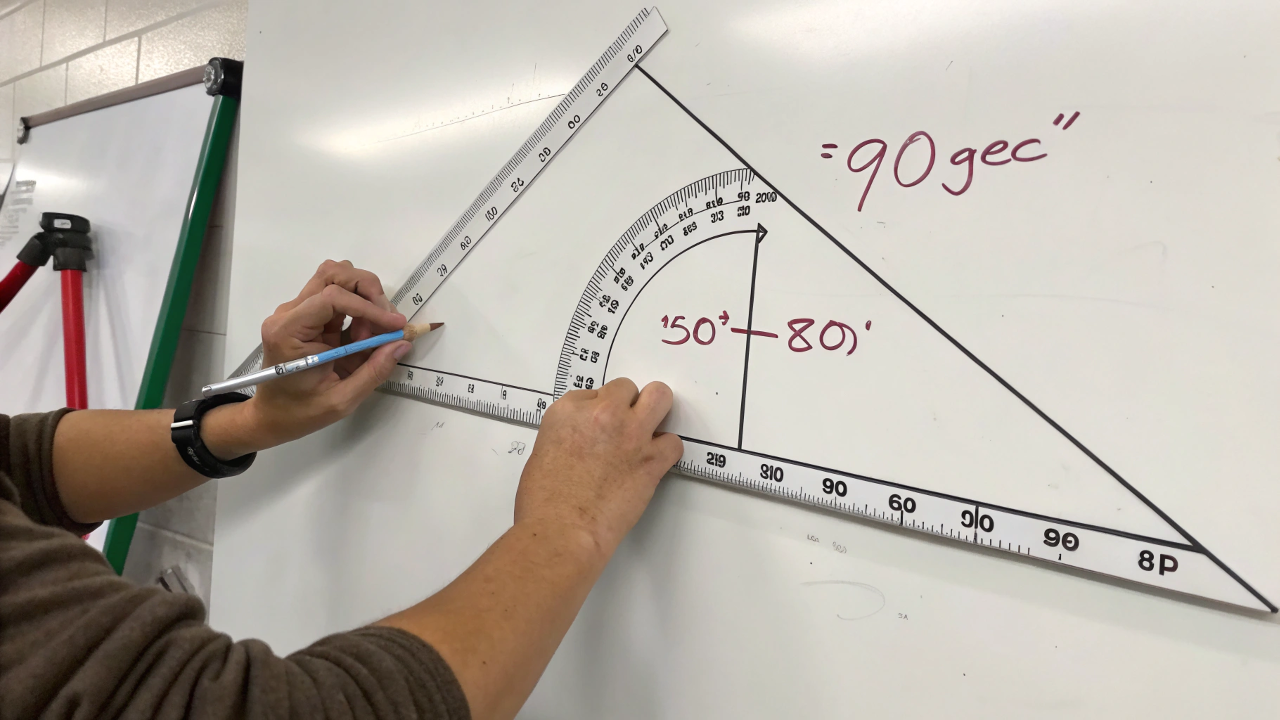
Mengukur dan membuat sudut siku-siku adalah keterampilan dasar yang berguna dalam berbagai situasi. Ada beberapa cara yang dapat digunakan untuk mengukur dan membuat sudut siku-siku, tergantung pada alat dan bahan yang tersedia. Berikut adalah beberapa metode yang umum digunakan:

• Menggunakan Siku-Siku: Siku-siku adalah alat yang dirancang khusus untuk mengukur dan membuat sudut siku-siku. Alat ini biasanya terbuat dari logam atau plastik dan memiliki dua sisi yang membentuk sudut 90 derajat. Untuk menggunakan siku-siku, cukup letakkan salah satu sisi pada garis yang sudah ada, lalu tarik garis sepanjang sisi lainnya untuk membuat sudut siku-siku.
• Menggunakan Busur Derajat: Busur derajat adalah alat yang digunakan untuk mengukur sudut dalam derajat. Untuk mengukur sudut siku-siku, letakkan titik tengah busur derajat pada titik sudut yang ingin diukur, lalu sejajarkan salah satu sisi sudut dengan garis 0 derajat. Jika sisi lainnya menunjukkan angka 90 derajat, maka sudut tersebut adalah sudut siku-siku.
• Menggunakan Teorema Pythagoras: Teorema Pythagoras dapat digunakan untuk membuat sudut siku-siku dengan menggunakan tiga batang atau tali dengan panjang yang berbeda. Misalnya, jika kita memiliki tiga batang dengan panjang 3 cm, 4 cm, dan 5 cm, maka kita dapat membentuk segitiga siku-siku dengan menempatkan batang terpanjang (5 cm) sebagai sisi miring, dan dua batang lainnya (3 cm dan 4 cm) sebagai sisi-sisi yang membentuk sudut siku-siku.
• Menggunakan Aplikasi Smartphone: Saat ini, banyak aplikasi smartphone yang dapat digunakan untuk mengukur sudut. Aplikasi ini biasanya menggunakan sensor accelerometer dan gyroscope pada smartphone untuk menentukan sudut kemiringan. Untuk mengukur sudut siku-siku, cukup letakkan smartphone pada permukaan yang ingin diukur, lalu ikuti instruksi pada aplikasi.

Sudut Siku-Siku dalam Matematika Tingkat Lanjut

Meskipun tampak sederhana, sudut siku-siku juga memainkan peran penting dalam matematika tingkat lanjut. Dalam geometri non-Euclidean, konsep sudut siku-siku dapat berbeda dari yang kita kenal dalam geometri Euclidean. Misalnya, dalam geometri bola, garis lurus didefinisikan sebagai lingkaran besar, dan sudut siku-siku dapat memiliki ukuran yang berbeda dari 90 derajat.

Dalam kalkulus, sudut siku-siku digunakan dalam definisi integral garis dan integral permukaan. Integral garis digunakan untuk menghitung panjang kurva, sedangkan integral permukaan digunakan untuk menghitung luas permukaan. Kedua jenis integral ini melibatkan perhitungan sudut antara vektor normal dan vektor tangen, yang seringkali merupakan sudut siku-siku.

Dalam aljabar linear, sudut siku-siku terkait erat dengan konsep ortogonalitas. Dua vektor dikatakan ortogonal jika hasil kali titik (dot product) mereka sama dengan nol. Secara geometris, ini berarti bahwa kedua vektor tersebut saling tegak lurus, atau membentuk sudut siku-siku.

Kesalahan Umum tentang Sudut Siku-Siku

Meskipun sudut siku-siku adalah konsep yang mendasar, ada beberapa kesalahan umum yang sering terjadi dalam pemahaman dan penggunaannya. Berikut adalah beberapa kesalahan umum tentang sudut siku-siku:

• Menganggap Semua Sudut 90 Derajat adalah Sudut Siku-Siku: Meskipun semua sudut siku-siku memiliki ukuran 90 derajat, tidak semua sudut 90 derajat adalah sudut siku-siku. Misalnya, dalam geometri non-Euclidean, sudut 90 derajat dapat memiliki sifat yang berbeda dari sudut siku-siku dalam geometri Euclidean.
• Menggunakan Siku-Siku yang Tidak Akurat: Siku-siku yang tidak akurat dapat menghasilkan sudut yang tidak tepat 90 derajat. Hal ini dapat menyebabkan kesalahan dalam konstruksi, pertukangan kayu, dan desain grafis. Oleh karena itu, penting untuk menggunakan siku-siku yang berkualitas baik dan terkalibrasi dengan benar.
• Tidak Memperhatikan Toleransi: Dalam aplikasi praktis, seringkali ada toleransi yang diizinkan dalam pengukuran sudut. Artinya, sudut yang sedikit berbeda dari 90 derajat masih dapat dianggap sebagai sudut siku-siku, tergantung pada tingkat presisi yang dibutuhkan.
• Mengabaikan Pengaruh Lingkungan: Faktor-faktor lingkungan seperti suhu dan kelembaban dapat mempengaruhi ukuran dan bentuk benda, termasuk sudut siku-siku. Oleh karena itu, penting untuk mempertimbangkan pengaruh lingkungan saat mengukur dan membuat sudut siku-siku dalam kondisi yang ekstrem.

Tips dan Trik dalam Menggunakan Sudut Siku-Siku

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam menggunakan sudut siku-siku secara efektif:

• Gunakan Alat yang Tepat: Pilih alat yang tepat untuk mengukur dan membuat sudut siku-siku, tergantung pada aplikasi dan tingkat presisi yang dibutuhkan. Siku-siku, busur derajat, dan aplikasi smartphone adalah beberapa pilihan yang tersedia.
• Periksa Akurasi Alat: Pastikan bahwa alat yang Anda gunakan akurat dan terkalibrasi dengan benar. Siku-siku yang tidak akurat dapat menghasilkan sudut yang salah, yang dapat menyebabkan masalah dalam konstruksi dan desain.
• Perhatikan Toleransi: Pertimbangkan toleransi yang diizinkan dalam pengukuran sudut. Dalam beberapa aplikasi, sudut yang sedikit berbeda dari 90 derajat masih dapat diterima.
• Gunakan Teknik yang Tepat: Gunakan teknik yang tepat untuk mengukur dan membuat sudut siku-siku. Misalnya, saat menggunakan siku-siku, pastikan bahwa sisi-sisinya sejajar dengan garis yang ingin Anda ukur atau buat.
• Perhatikan Pengaruh Lingkungan: Pertimbangkan pengaruh lingkungan seperti suhu dan kelembaban saat mengukur dan membuat sudut siku-siku. Faktor-faktor ini dapat mempengaruhi ukuran dan bentuk benda.
• Latih Keterampilan Anda: Semakin sering Anda berlatih mengukur dan membuat sudut siku-siku, semakin terampil Anda dalam melakukannya. Latihan akan membantu Anda mengembangkan intuisi dan kepekaan terhadap sudut siku-siku.

Kesimpulan

Sudut siku-siku adalah konsep fundamental dalam geometri yang memiliki banyak penerapan praktis dalam kehidupan sehari-hari. Dari arsitektur dan konstruksi hingga desain grafis dan navigasi, sudut siku-siku hadir di sekitar kita dalam berbagai bentuk dan fungsi. Memahami definisi, karakteristik, dan sifat-sifat sudut siku-siku akan membuka wawasan baru tentang bagaimana bentuk dan ruang saling berinteraksi. Dengan menggunakan alat dan teknik yang tepat, serta memperhatikan faktor-faktor lingkungan, kita dapat mengukur dan membuat sudut siku-siku dengan akurat dan efektif. Sudut siku-siku bukan hanya konsep abstrak dalam matematika, tetapi juga alat yang ampuh untuk memecahkan masalah dan menciptakan solusi dalam berbagai bidang.

Pemahaman yang mendalam tentang sudut siku-siku juga penting dalam matematika tingkat lanjut, seperti geometri non-Euclidean, kalkulus, dan aljabar linear. Dalam bidang-bidang ini, sudut siku-siku terkait erat dengan konsep-konsep seperti ortogonalitas, integral garis, dan integral permukaan. Dengan menguasai konsep sudut siku-siku, kita dapat membuka pintu menuju pemahaman yang lebih mendalam tentang matematika dan aplikasinya dalam dunia nyata.

Oleh karena itu, mari kita terus belajar dan mengembangkan pemahaman kita tentang sudut siku-siku, serta menerapkannya dalam berbagai aspek kehidupan kita. Dengan demikian, kita dapat memanfaatkan kekuatan sudut siku-siku untuk menciptakan dunia yang lebih teratur, efisien, dan indah.

Berikut adalah tabel yang merangkum informasi penting tentang sudut siku-siku:

Fitur	Deskripsi
Definisi	Sudut yang besarnya tepat 90 derajat
Simbol	Kotak kecil di titik sudut
Sifat	Dua garis yang membentuk sudut siku-siku saling tegak lurus
Penerapan	Arsitektur, konstruksi, pertukangan kayu, desain grafis, navigasi, perangkat rumah tangga
Alat Pengukur	Siku-siku, busur derajat, aplikasi smartphone
Matematika Tingkat Lanjut	Geometri non-Euclidean, kalkulus, aljabar linear

Semoga artikel ini memberikan pemahaman yang komprehensif tentang sudut siku-siku dan aplikasinya dalam berbagai bidang. Teruslah belajar dan bereksplorasi, dan jangan ragu untuk bertanya jika Anda memiliki pertanyaan lebih lanjut.