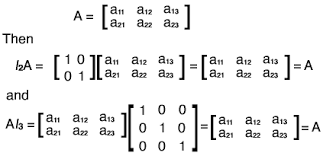Matriks Identitas: Alat untuk Mengorganisir Data

DALAM dunia yang dipenuhi informasi, kemampuan untuk menyusun dan memahami data menjadi semakin krusial. Salah satu alat yang sangat berguna dalam bidang matematika, ilmu komputer, dan berbagai disiplin ilmu lainnya adalah matriks identitas. Matriks ini, meskipun tampak sederhana, memiliki peran fundamental dalam berbagai operasi dan konsep. Mari kita selami lebih dalam mengenai apa itu matriks identitas, bagaimana ia bekerja, dan mengapa ia begitu penting.

Definisi dan Sifat Dasar Matriks Identitas

Matriks identitas, yang juga dikenal sebagai matriks satuan, adalah sebuah matriks persegi di mana semua elemen pada diagonal utamanya bernilai 1, sementara semua elemen lainnya bernilai 0. Diagonal utama adalah garis yang membentang dari sudut kiri atas hingga sudut kanan bawah matriks. Ukuran matriks identitas ditentukan oleh jumlah baris dan kolomnya, yang selalu sama karena ia adalah matriks persegi. Matriks identitas dengan ukuran n x n sering dilambangkan dengan simbol I_n.

Sebagai contoh, matriks identitas berukuran 2x2 adalah:

1	0
0	1

Dan matriks identitas berukuran 3x3 adalah:

1	0	0
0	1	0
0	0	1

Sifat paling mendasar dari matriks identitas adalah ketika dikalikan dengan matriks lain, ia tidak mengubah matriks tersebut. Ini mirip dengan angka 1 dalam perkalian bilangan real. Secara matematis, jika A adalah matriks sembarang dan I adalah matriks identitas dengan ukuran yang sesuai, maka:

A I = A

I A = A

Sifat ini menjadikan matriks identitas sebagai elemen netral dalam operasi perkalian matriks.

Peran Penting dalam Aljabar Linear

Dalam aljabar linear, matriks identitas memegang peranan krusial dalam berbagai konsep dan operasi. Beberapa di antaranya adalah:

1. Invers Matriks: Konsep invers matriks sangat penting dalam menyelesaikan sistem persamaan linear dan transformasi linear. Sebuah matriks A dikatakan memiliki invers (A^-1) jika dan hanya jika hasil perkalian A dengan A^-1 menghasilkan matriks identitas: A A^-1 = A^-1 A = I. Matriks identitas menjadi titik referensi untuk menentukan apakah sebuah matriks memiliki invers atau tidak.
2. Transformasi Linear: Transformasi linear adalah fungsi yang memetakan vektor dari satu ruang vektor ke ruang vektor lainnya, sambil mempertahankan operasi penjumlahan vektor dan perkalian skalar. Matriks identitas merepresentasikan transformasi linear identitas, yaitu transformasi yang tidak mengubah vektor sama sekali. Dalam kata lain, jika sebuah vektor dikalikan dengan matriks identitas, vektor tersebut tetap sama.
3. Basis dan Dimensi: Dalam ruang vektor, basis adalah himpunan vektor linear independen yang dapat digunakan untuk merepresentasikan semua vektor lain dalam ruang tersebut. Matriks identitas dapat digunakan untuk membentuk basis ortonormal, yaitu basis di mana semua vektornya saling tegak lurus dan memiliki panjang satuan. Basis ortonormal sangat berguna dalam berbagai aplikasi, seperti dekomposisi nilai singular (SVD) dan analisis komponen utama (PCA).
4. Nilai Eigen dan Vektor Eigen: Nilai eigen dan vektor eigen adalah konsep penting dalam analisis matriks. Nilai eigen adalah skalar yang terkait dengan matriks, sedangkan vektor eigen adalah vektor yang tidak berubah arah ketika dikalikan dengan matriks tersebut. Matriks identitas digunakan dalam perhitungan nilai eigen dan vektor eigen, khususnya dalam menyelesaikan persamaan karakteristik matriks.

Aplikasi dalam Ilmu Komputer

Selain dalam matematika, matriks identitas juga memiliki banyak aplikasi penting dalam ilmu komputer. Beberapa di antaranya adalah:

1. Grafika Komputer: Dalam grafika komputer, matriks digunakan untuk merepresentasikan transformasi geometris, seperti translasi, rotasi, dan penskalaan. Matriks identitas merepresentasikan transformasi identitas, yaitu transformasi yang tidak mengubah objek sama sekali. Matriks identitas digunakan sebagai titik awal untuk membangun transformasi yang lebih kompleks.
2. Pengolahan Citra: Dalam pengolahan citra, matriks digunakan untuk merepresentasikan gambar dan melakukan berbagai operasi, seperti filtering, segmentasi, dan pengenalan objek. Matriks identitas dapat digunakan sebagai kernel dalam operasi konvolusi, yang merupakan operasi dasar dalam pengolahan citra.
3. Kriptografi: Dalam kriptografi, matriks digunakan dalam berbagai algoritma enkripsi dan dekripsi. Matriks identitas dapat digunakan sebagai kunci atau bagian dari kunci dalam beberapa algoritma kriptografi.
4. Pembelajaran Mesin: Dalam pembelajaran mesin, matriks digunakan untuk merepresentasikan data dan model. Matriks identitas digunakan dalam berbagai algoritma pembelajaran mesin, seperti regresi linear, klasifikasi, dan pengelompokan. Misalnya, dalam regularisasi Ridge Regression, matriks identitas ditambahkan ke matriks kovarians fitur untuk mencegah overfitting.

Contoh Penggunaan Matriks Identitas

Untuk memberikan gambaran yang lebih jelas tentang bagaimana matriks identitas digunakan dalam praktik, berikut adalah beberapa contoh:

1. Menyelesaikan Sistem Persamaan Linear: Misalkan kita memiliki sistem persamaan linear berikut:

   2x + y = 5

   x - y = 1

   Sistem ini dapat ditulis dalam bentuk matriks sebagai berikut:

   A x = b

   Di mana:

   A =

   2	1
   1	-1

   x =

   x

   y

   b =

   5

   1

   Untuk menyelesaikan sistem ini, kita perlu mencari invers dari matriks A (A^-1). Jika kita berhasil menemukan A^-1, maka solusi dari sistem persamaan adalah:

   x = A^-1 b

   Proses mencari invers matriks melibatkan penggunaan matriks identitas sebagai titik referensi.

2. Rotasi Objek dalam Grafika Komputer: Misalkan kita ingin memutar sebuah objek 2D sebesar 30 derajat searah jarum jam. Kita dapat menggunakan matriks rotasi berikut:

    

   R =

   cos(30°)	-sin(30°)
   sin(30°)	cos(30°)

   Jika kita ingin memutar objek kembali ke posisi semula, kita perlu melakukan rotasi sebesar -30 derajat. Matriks rotasi untuk -30 derajat adalah invers dari matriks rotasi untuk 30 derajat. Jika kita mengalikan kedua matriks rotasi ini, kita akan mendapatkan matriks identitas, yang berarti objek kembali ke posisi semula.

3. Regularisasi Ridge Regression dalam Pembelajaran Mesin: Dalam Ridge Regression, kita menambahkan penalti pada model untuk mencegah overfitting. Penalti ini proporsional dengan kuadrat dari norma L2 dari koefisien model. Secara matematis, fungsi biaya Ridge Regression adalah:

    

   J(θ) = MSE(θ) + λ ||θ||²

   Di mana:

   MSE(θ) adalah Mean Squared Error

   θ adalah vektor koefisien model

   λ adalah parameter regularisasi

   ||θ||² adalah kuadrat dari norma L2 dari θ

   Dalam menyelesaikan persamaan normal untuk Ridge Regression, kita menambahkan matriks identitas dikalikan dengan parameter regularisasi (λI) ke matriks kovarians fitur. Ini membantu menstabilkan solusi dan mencegah overfitting.

Keterbatasan dan Pertimbangan

Meskipun matriks identitas memiliki banyak kegunaan, penting untuk memahami keterbatasannya dan mempertimbangkan beberapa hal:

1. Hanya Berlaku untuk Matriks Persegi: Matriks identitas hanya didefinisikan untuk matriks persegi, yaitu matriks dengan jumlah baris dan kolom yang sama. Ini berarti bahwa matriks identitas tidak dapat digunakan dengan matriks non-persegi.
2. Tidak Semua Matriks Memiliki Invers: Tidak semua matriks persegi memiliki invers. Matriks yang tidak memiliki invers disebut matriks singular. Matriks identitas digunakan untuk menentukan apakah sebuah matriks memiliki invers atau tidak. Jika determinan sebuah matriks adalah nol, maka matriks tersebut singular dan tidak memiliki invers.
3. Komputasi Invers Matriks Bisa Mahal: Menghitung invers matriks bisa menjadi operasi yang mahal secara komputasi, terutama untuk matriks berukuran besar. Ada berbagai algoritma untuk menghitung invers matriks, tetapi kompleksitas waktu mereka bervariasi.

Kesimpulan

Matriks identitas adalah alat yang fundamental dan serbaguna dalam matematika, ilmu komputer, dan berbagai disiplin ilmu lainnya. Sifatnya yang unik sebagai elemen netral dalam perkalian matriks menjadikannya penting dalam berbagai konsep dan operasi, seperti invers matriks, transformasi linear, dan basis ruang vektor. Dalam ilmu komputer, matriks identitas digunakan dalam grafika komputer, pengolahan citra, kriptografi, dan pembelajaran mesin. Meskipun memiliki keterbatasan, matriks identitas tetap menjadi alat yang sangat berharga untuk mengorganisir dan memanipulasi data.

Pemahaman yang mendalam tentang matriks identitas dan sifat-sifatnya sangat penting bagi siapa pun yang bekerja dengan data dan model matematika. Dengan memahami bagaimana matriks identitas bekerja, kita dapat mengembangkan solusi yang lebih efisien dan efektif untuk berbagai masalah.

Di masa depan, seiring dengan perkembangan teknologi dan semakin kompleksnya data yang kita hadapi, peran matriks identitas akan semakin penting. Oleh karena itu, investasi dalam pemahaman konsep ini akan memberikan manfaat jangka panjang bagi para profesional di berbagai bidang.

Semoga artikel ini memberikan wawasan yang bermanfaat tentang matriks identitas dan aplikasinya. Teruslah belajar dan menjelajahi dunia matematika dan ilmu komputer yang menarik! (H-2)