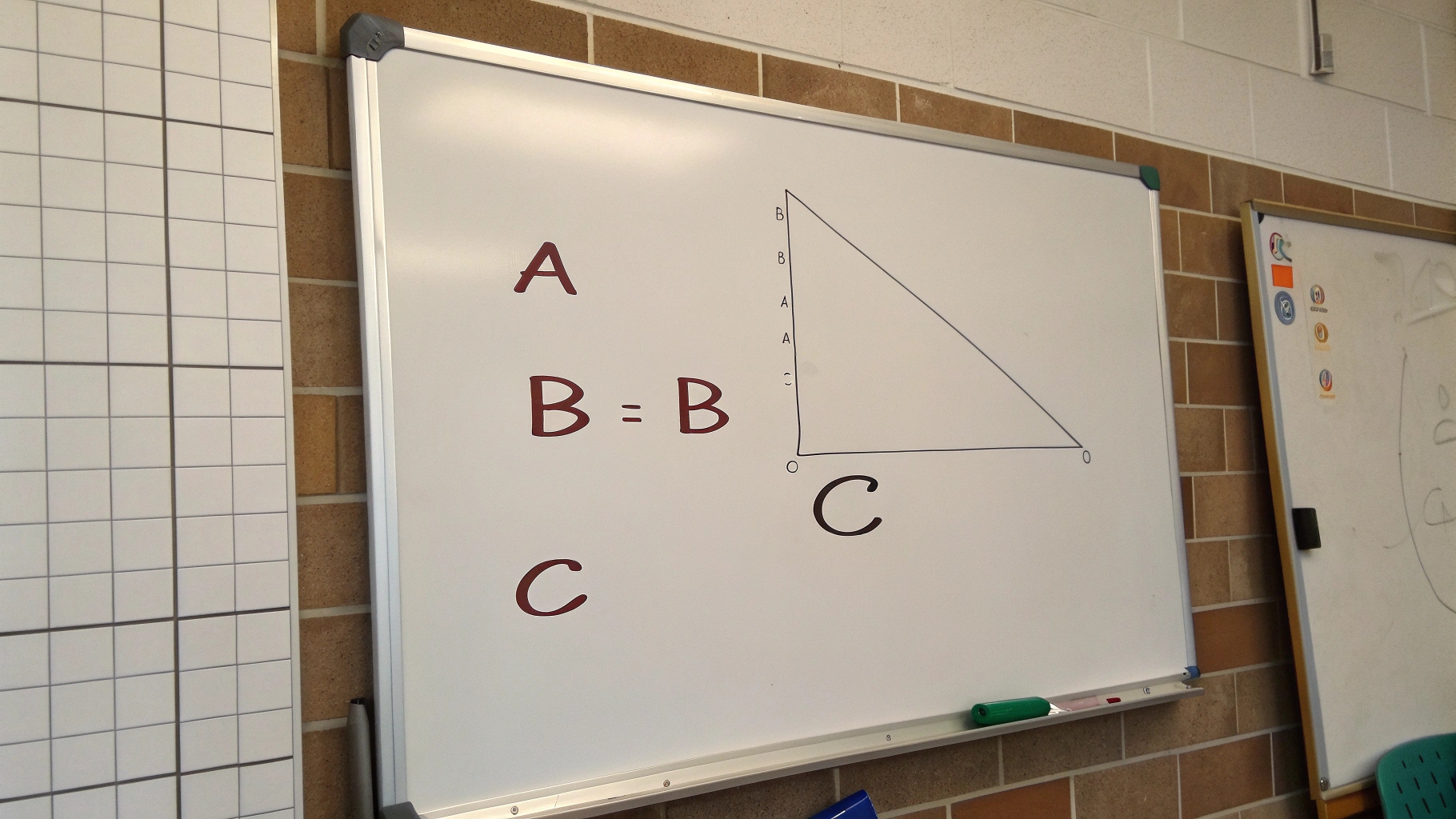Rumus Sudut Segitiga Siku-Siku yang Harus Diketahui

Segitiga siku-siku, sebuah bangun geometri fundamental, memegang peranan krusial dalam berbagai bidang, mulai dari matematika murni hingga aplikasi praktis dalam kehidupan sehari-hari. Keistimewaannya terletak pada keberadaan satu sudut yang tepat 90 derajat, yang memberikan karakteristik unik dan memungkinkan penerapan rumus-rumus khusus untuk menghitung sisi dan sudutnya. Memahami rumus-rumus ini bukan hanya penting bagi pelajar dan mahasiswa, tetapi juga bagi para profesional di bidang teknik, arsitektur, dan ilmu pengetahuan alam.

Memahami Dasar Segitiga Siku-Siku

Sebelum menyelami rumus-rumus yang lebih kompleks, mari kita pahami terlebih dahulu komponen dasar dari segitiga siku-siku. Segitiga ini memiliki tiga sisi, sisi alas, sisi tegak (tinggi), dan sisi miring (hipotenusa). Sisi miring selalu berhadapan dengan sudut siku-siku dan merupakan sisi terpanjang dari segitiga tersebut. Sudut-sudut pada segitiga siku-siku, selain sudut siku-siku itu sendiri, adalah sudut lancip yang jumlahnya selalu 90 derajat. Hubungan antara sisi dan sudut inilah yang menjadi dasar bagi rumus-rumus trigonometri yang akan kita bahas.

Definisi Segitiga Siku-Siku, Segitiga yang salah satu sudutnya berukuran 90 derajat.

Komponen Segitiga Siku-Siku,

• Alas, Sisi yang menjadi dasar segitiga.
• Tinggi, Sisi yang tegak lurus dengan alas.
• Hipotenusa, Sisi terpanjang, berhadapan dengan sudut siku-siku.

Rumus Pythagoras, Fondasi Perhitungan Segitiga Siku-Siku

Rumus Pythagoras adalah salah satu teorema paling terkenal dan mendasar dalam geometri. Rumus ini menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang sisi alas dan sisi tegak. Secara matematis, rumus ini dapat dituliskan sebagai,

a² + b² = c²

di mana,

• a adalah panjang sisi alas
• b adalah panjang sisi tegak
• c adalah panjang sisi miring (hipotenusa)

Rumus Pythagoras sangat berguna untuk mencari panjang salah satu sisi segitiga siku-siku jika panjang dua sisi lainnya diketahui. Misalnya, jika kita mengetahui panjang sisi alas dan sisi tegak, kita dapat menghitung panjang sisi miring dengan mengakarkan jumlah kuadrat kedua sisi tersebut.

Contoh Soal, Sebuah segitiga siku-siku memiliki sisi alas sepanjang 3 cm dan sisi tegak sepanjang 4 cm. Hitunglah panjang sisi miringnya.

Penyelesaian,

c² = a² + b²

c² = 3² + 4²

c² = 9 + 16

c² = 25

c = √25

c = 5 cm

Jadi, panjang sisi miring segitiga tersebut adalah 5 cm.

Rumus Trigonometri Dasar, Sinus, Cosinus, dan Tangen

Selain Rumus Pythagoras, trigonometri juga memainkan peran penting dalam perhitungan segitiga siku-siku. Trigonometri mempelajari hubungan antara sudut dan sisi pada segitiga. Tiga fungsi trigonometri dasar yang sering digunakan adalah sinus (sin), cosinus (cos), dan tangen (tan). Ketiga fungsi ini didefinisikan sebagai berikut,

• Sinus (sin), Perbandingan antara panjang sisi depan (sisi yang berhadapan dengan sudut) dengan panjang sisi miring (hipotenusa).
• Cosinus (cos), Perbandingan antara panjang sisi samping (sisi yang berdekatan dengan sudut) dengan panjang sisi miring (hipotenusa).
• Tangen (tan), Perbandingan antara panjang sisi depan (sisi yang berhadapan dengan sudut) dengan panjang sisi samping (sisi yang berdekatan dengan sudut).

Secara matematis, fungsi-fungsi trigonometri ini dapat dituliskan sebagai,

• sin θ = depan / miring
• cos θ = samping / miring
• tan θ = depan / samping

di mana θ adalah sudut yang diukur.

Mnemonic untuk Mengingat, SOH CAH TOA (Sin Opposite Hypotenuse, Cos Adjacent Hypotenuse, Tan Opposite Adjacent)

Dengan menggunakan fungsi-fungsi trigonometri ini, kita dapat menghitung besar sudut pada segitiga siku-siku jika panjang sisi-sisinya diketahui, atau sebaliknya, menghitung panjang sisi jika besar sudut dan panjang salah satu sisi diketahui.

Contoh Soal, Sebuah segitiga siku-siku memiliki sisi depan sepanjang 6 cm dan sisi miring sepanjang 10 cm. Hitunglah nilai sinus sudut tersebut.

Penyelesaian,

sin θ = depan / miring

sin θ = 6 / 10

sin θ = 0.6

Jadi, nilai sinus sudut tersebut adalah 0.6.

Rumus Sudut Istimewa, Mempermudah Perhitungan

Dalam trigonometri, terdapat beberapa sudut istimewa yang memiliki nilai sinus, cosinus, dan tangen yang mudah diingat. Sudut-sudut istimewa ini adalah 0°, 30°, 45°, 60°, dan 90°. Mengetahui nilai-nilai trigonometri untuk sudut-sudut istimewa ini dapat mempermudah perhitungan dan mempercepat penyelesaian soal-soal yang melibatkan segitiga siku-siku.

Berikut adalah tabel nilai trigonometri untuk sudut-sudut istimewa,

Sudut (°)	Sinus	Cosinus	Tangen
0	0	1	0
30	1/2	√3/2	√3/3
45	√2/2	√2/2	1
60	√3/2	1/2	√3
90	1	0	Tak Terdefinisi

Contoh Soal, Sebuah segitiga siku-siku memiliki sudut 30° dan sisi miring sepanjang 8 cm. Hitunglah panjang sisi depan sudut tersebut.

Penyelesaian,

sin 30° = depan / miring

1/2 = depan / 8

depan = 8 (1/2)

depan = 4 cm

Jadi, panjang sisi depan sudut tersebut adalah 4 cm.

Aplikasi Rumus Segitiga Siku-Siku dalam Kehidupan Sehari-hari

Rumus-rumus segitiga siku-siku tidak hanya berguna dalam matematika, tetapi juga memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Berikut adalah beberapa contohnya,

• Konstruksi Bangunan, Arsitek dan insinyur menggunakan rumus segitiga siku-siku untuk menghitung tinggi bangunan, kemiringan atap, dan jarak antar komponen struktural.
• Navigasi, Pilot dan pelaut menggunakan trigonometri untuk menentukan posisi, arah, dan jarak tempuh.
• Pemetaan, Surveyor menggunakan rumus segitiga siku-siku untuk mengukur luas tanah dan membuat peta.
• Fisika, Fisikawan menggunakan trigonometri untuk menganalisis gerak proyektil, gelombang, dan gaya.
• Desain Grafis, Desainer grafis menggunakan trigonometri untuk membuat gambar perspektif dan animasi.

Contoh Aplikasi, Seorang tukang ingin membuat tangga dengan kemiringan 45°. Jika tinggi dinding yang akan dipanjat tangga adalah 3 meter, berapa panjang tangga yang dibutuhkan?

Penyelesaian,

Kita dapat menggunakan fungsi sinus untuk menyelesaikan masalah ini.

sin 45° = tinggi / panjang tangga

√2/2 = 3 / panjang tangga

panjang tangga = 3 / (√2/2)

panjang tangga = 3 (2/√2)

panjang tangga = 3√2 meter

panjang tangga ≈ 4.24 meter

Jadi, tukang tersebut membutuhkan tangga sepanjang sekitar 4.24 meter.

Rumus Luas dan Keliling Segitiga Siku-Siku

Selain menghitung sisi dan sudut, kita juga sering perlu menghitung luas dan keliling segitiga siku-siku. Rumus untuk menghitung luas dan keliling segitiga siku-siku adalah sebagai berikut,

• Luas, 1/2 alas tinggi
• Keliling, alas + tinggi + hipotenusa

Contoh Soal, Sebuah segitiga siku-siku memiliki sisi alas sepanjang 5 cm, sisi tegak sepanjang 12 cm, dan sisi miring sepanjang 13 cm. Hitunglah luas dan keliling segitiga tersebut.

Penyelesaian,

Luas,

Luas = 1/2 alas tinggi

Luas = 1/2 5 12

Luas = 30 cm²

Keliling,

Keliling = alas + tinggi + hipotenusa

Keliling = 5 + 12 + 13

Keliling = 30 cm

Jadi, luas segitiga tersebut adalah 30 cm² dan kelilingnya adalah 30 cm.

Rumus Tambahan, Fungsi Trigonometri Kebalikan

Selain fungsi sinus, cosinus, dan tangen, terdapat juga fungsi trigonometri kebalikan, yaitu cosecan (csc), secan (sec), dan cotangen (cot). Fungsi-fungsi ini didefinisikan sebagai berikut,

• Cosecan (csc), Kebalikan dari sinus (csc θ = 1 / sin θ)
• Secan (sec), Kebalikan dari cosinus (sec θ = 1 / cos θ)
• Cotangen (cot), Kebalikan dari tangen (cot θ = 1 / tan θ)

Fungsi-fungsi trigonometri kebalikan ini berguna dalam beberapa kasus, terutama ketika kita ingin mencari nilai sudut jika diketahui perbandingan sisi yang tidak langsung berhubungan dengan sinus, cosinus, atau tangen.

Tips dan Trik dalam Menyelesaikan Soal Segitiga Siku-Siku

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam menyelesaikan soal-soal yang melibatkan segitiga siku-siku,

• Gambarkan Segitiga, Selalu gambarkan segitiga siku-siku terlebih dahulu untuk memvisualisasikan masalah dan mengidentifikasi sisi dan sudut yang diketahui.
• Identifikasi Rumus yang Tepat, Pilih rumus yang sesuai dengan informasi yang diketahui dan yang ingin dicari.
• Gunakan Kalkulator, Gunakan kalkulator untuk menghitung nilai trigonometri dan akar kuadrat.
• Periksa Jawaban, Pastikan jawaban Anda masuk akal dan sesuai dengan konteks soal. Misalnya, panjang sisi tidak mungkin negatif.
• Latihan Soal, Semakin banyak Anda berlatih, semakin mahir Anda dalam menyelesaikan soal-soal segitiga siku-siku.

Kesalahan Umum yang Perlu Dihindari

Berikut adalah beberapa kesalahan umum yang sering dilakukan dalam menyelesaikan soal-soal segitiga siku-siku,

• Salah Mengidentifikasi Sisi, Pastikan Anda mengidentifikasi sisi depan, samping, dan miring dengan benar, terutama ketika menggunakan fungsi trigonometri.
• Salah Menggunakan Rumus, Pastikan Anda menggunakan rumus yang tepat untuk situasi yang diberikan.
• Lupa Satuan, Jangan lupa untuk menyertakan satuan yang tepat dalam jawaban Anda.
• Pembulatan yang Terlalu Dini, Hindari melakukan pembulatan terlalu dini dalam perhitungan, karena dapat menyebabkan kesalahan yang signifikan pada jawaban akhir.
• Tidak Memeriksa Jawaban, Selalu periksa jawaban Anda untuk memastikan bahwa jawaban tersebut masuk akal dan sesuai dengan konteks soal.

Kesimpulan

Memahami rumus-rumus segitiga siku-siku adalah kunci untuk menguasai geometri dan trigonometri. Dengan memahami Rumus Pythagoras, fungsi trigonometri dasar, dan sudut-sudut istimewa, Anda dapat menyelesaikan berbagai macam soal yang melibatkan segitiga siku-siku. Selain itu, pemahaman ini juga sangat berguna dalam berbagai aplikasi praktis dalam kehidupan sehari-hari, mulai dari konstruksi bangunan hingga navigasi. Teruslah berlatih dan jangan ragu untuk mencari bantuan jika Anda mengalami kesulitan. Dengan ketekunan dan latihan yang cukup, Anda pasti akan menguasai konsep ini dengan baik.

Semoga artikel ini bermanfaat dan membantu Anda dalam memahami rumus-rumus segitiga siku-siku. Selamat belajar!